Gambler's ruin
It is the famous Gambler's ruin example. In this example, we will present a gambler. A reluctant gambler is dragged to a casino by his friends. He takes only 50$ to gamble with. Since he does not know much about gambling, he decides to play roulette. At each spin, he places 25$ on red. If red occurs, he wins 25$. If black comes up, he loses his 25$. Therefore, the odds of winning are 50%. He will quit playing when he either has 0 money left or is up to 25$ (75$ total). The transition probability is shown below.
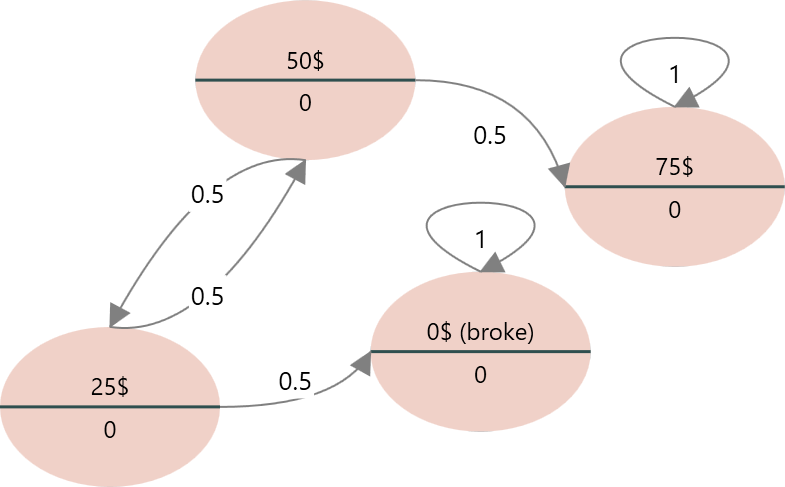
Let's model this process as a Markov Chain and examine its long-run behavior.
Start the Rational Will or the Decision Tree software and choose the Markov Model to start with.
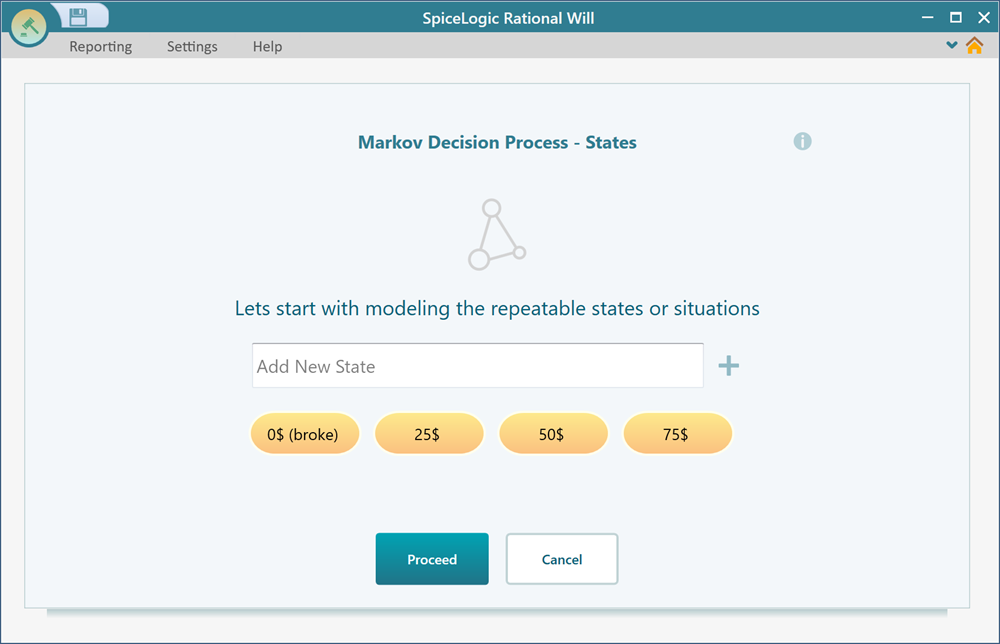
Step 1: Specifying the states
As soon as you click the "Markov model" button, you will see a wizard shows up. Set the 4 states as shown below in the first step of the wizard.
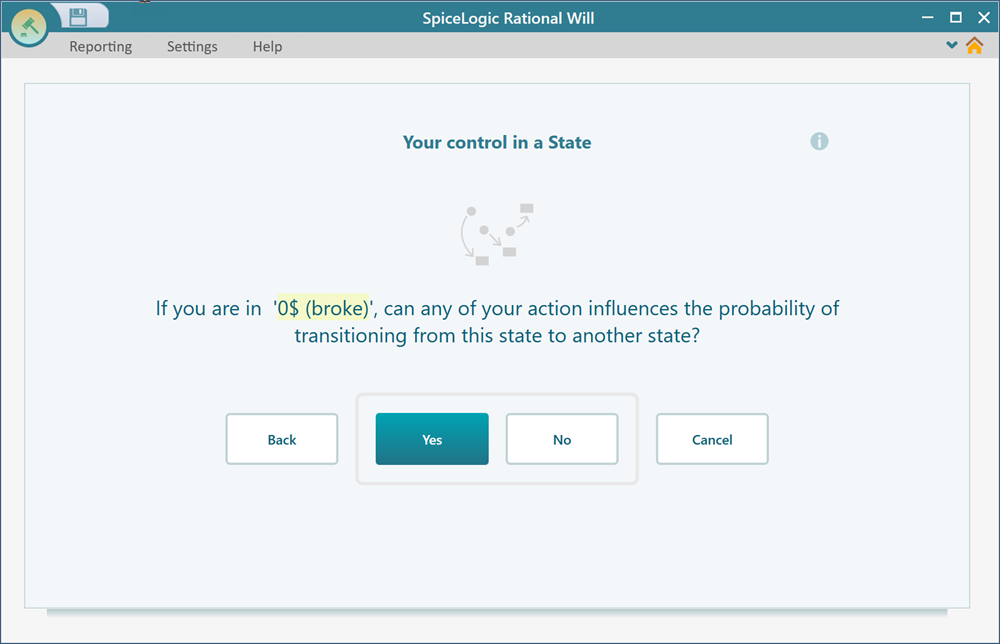
Then, in the next step, it will ask you if you want to add an Action to a given state. Simply set No. Do that for all states.
Step 2: Settings for cohort simulation
This is a step that will be shown up to let you fine-tune the Markov simulation. You can keep everything at its default value for this model and click "Proceed".
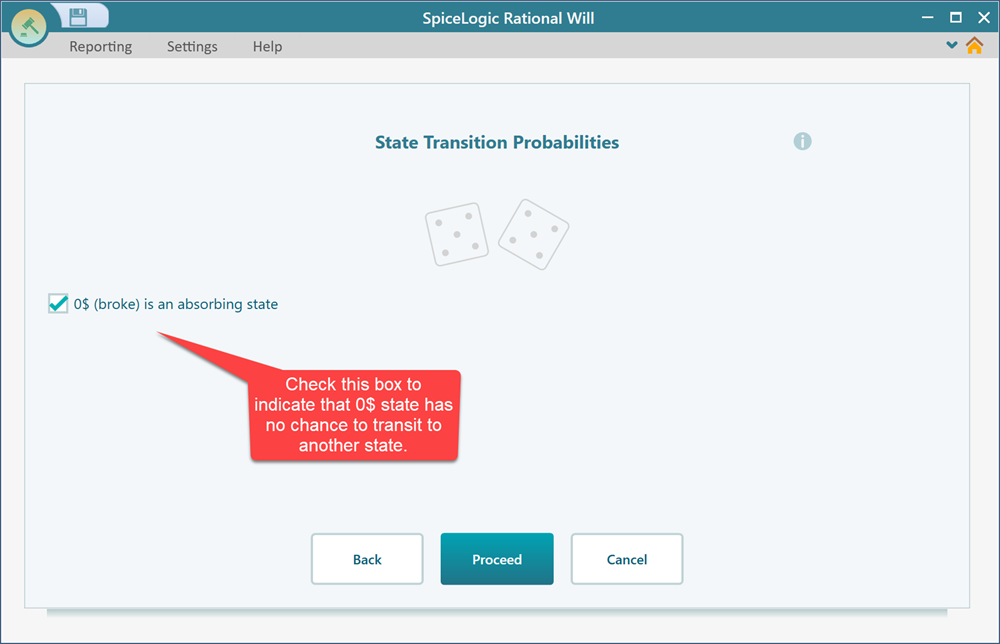
Step 3: Setting the transition probabilities
You will be presented to the transition probability setting window for each state one by one. Set the transition probabilities for the states as shown below. When you set the probabilities for a given state, click the 'Proceed' button.
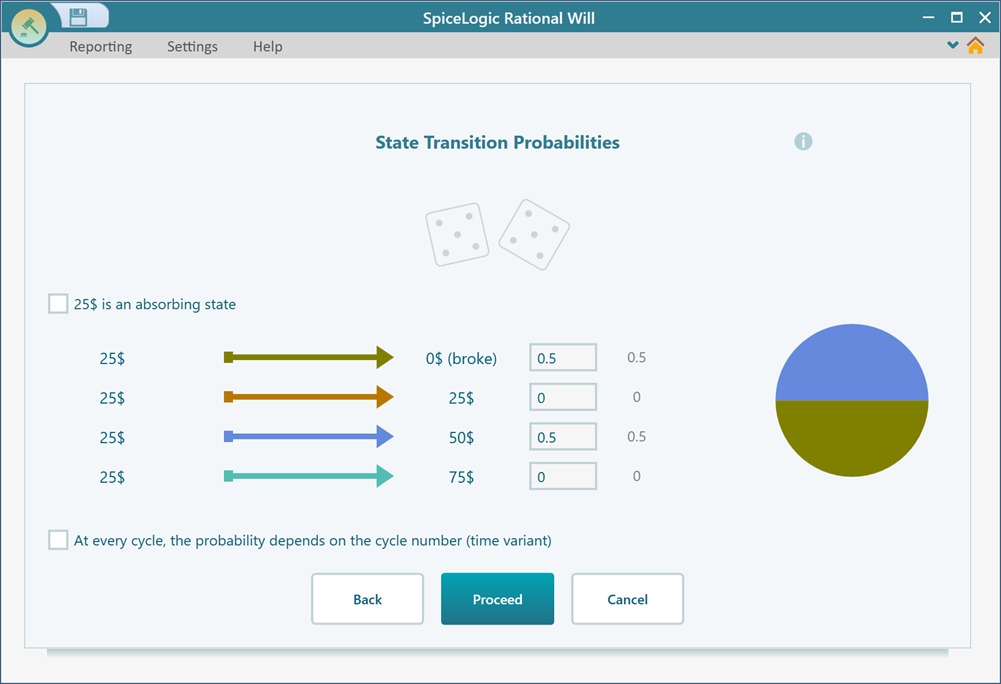
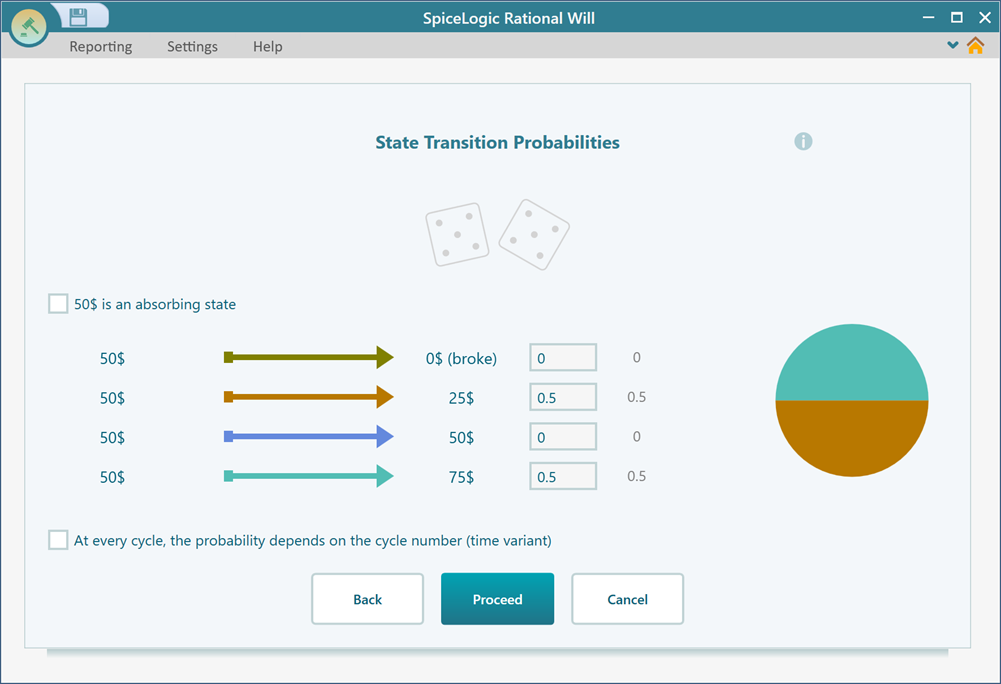
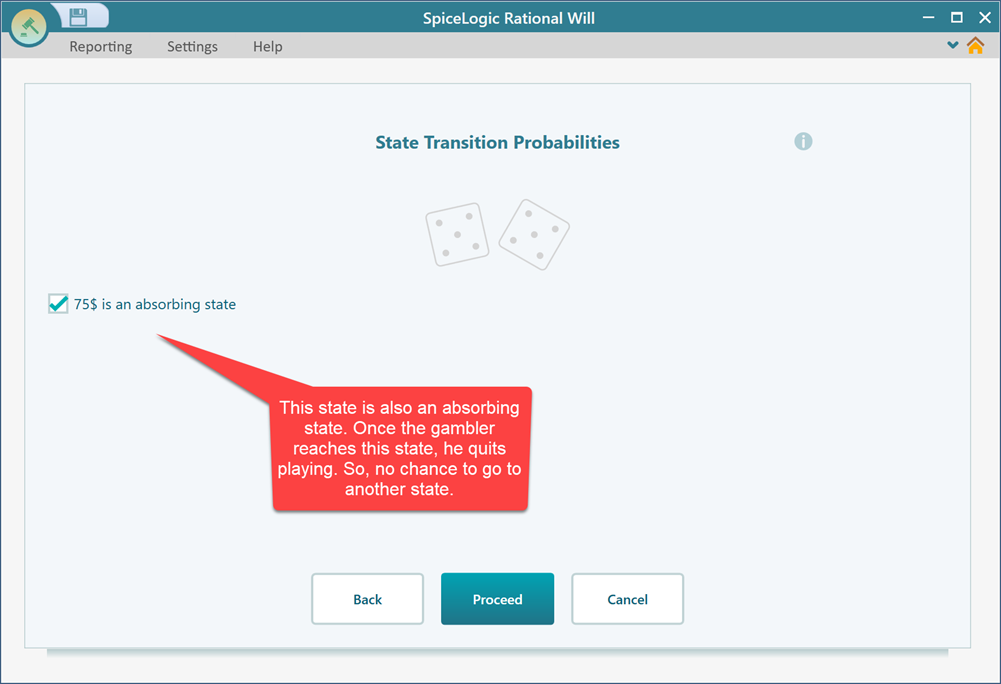
Step 4: Setting initial state
Once you click the "Proceed" button from the previous state, you will be asked to set the initial state. Set the 0$ state as the initial state. Then click proceed.
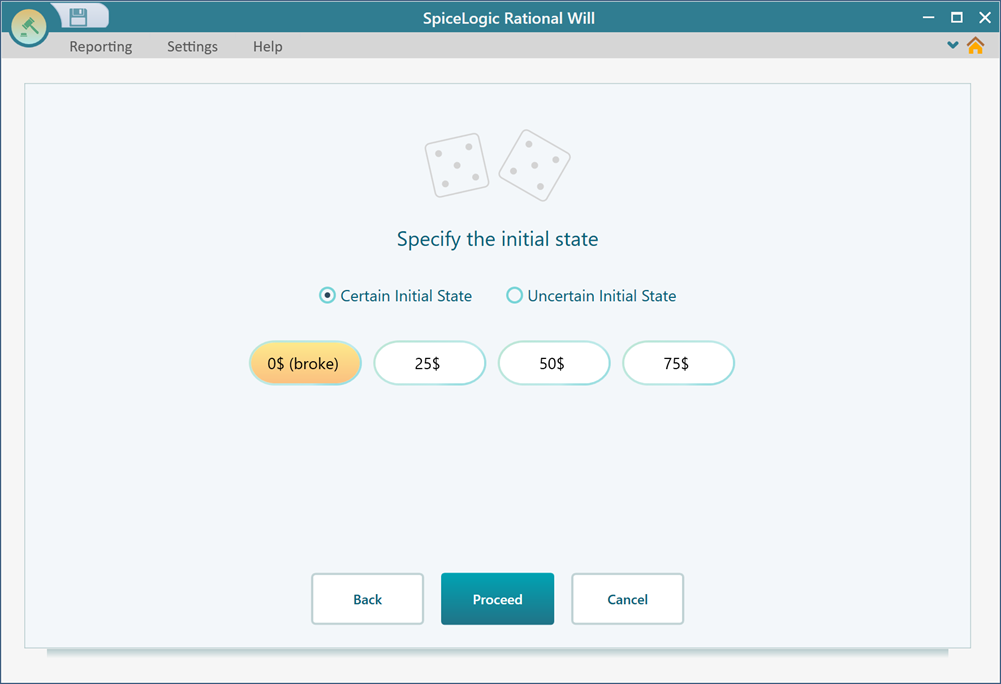
Once you click to proceed, you will be asked if you want to set any reward or payoff to any state. For this model, we do not need to set any payoff or reward. So, answer "No".
Step 5: Analyzing the result.
As soon as you click "No" in the previous step, you will see the Markov model generated as a Decision Tree diagram.
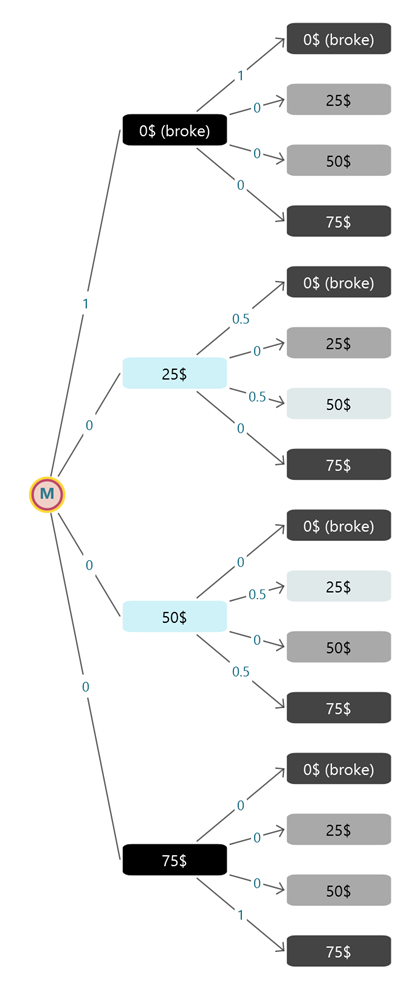
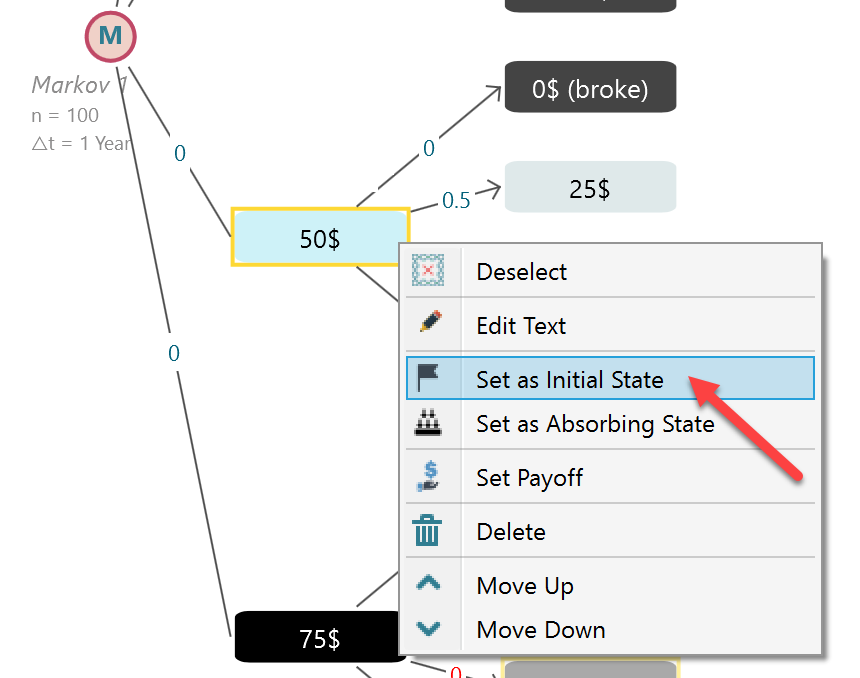
Now, you can analyze, what state the gambler will highly likely end up in based on how much money he starts with. Let's select the 50$ state as the initial state.
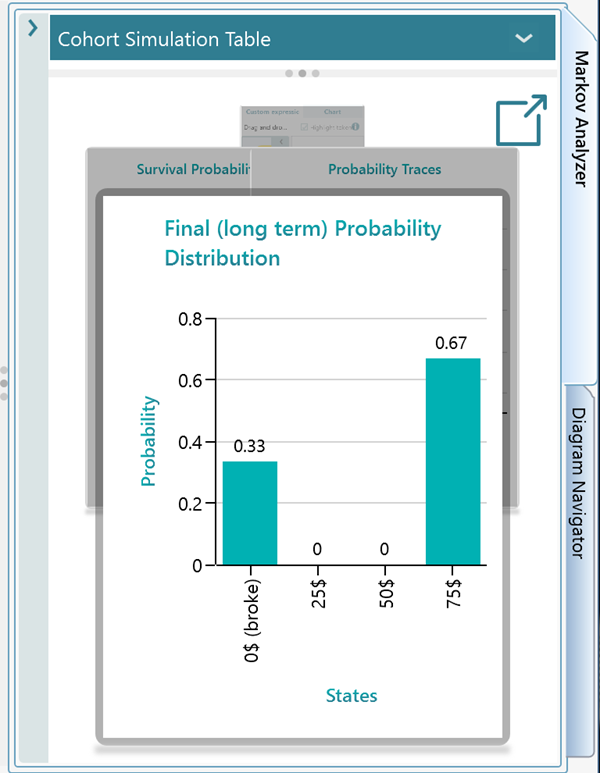
Now, open the Markov Analyzer panel. notice that the probability of getting broke is 33% and reaching 75$ state is 67%.
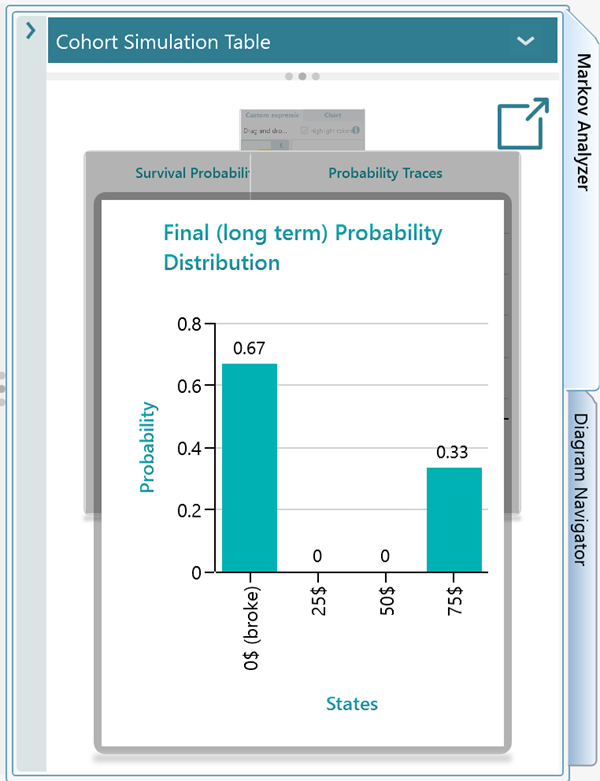
Now, let's change the initial state. Select the 25$ state and set it as the initial set from the right mouse click the context menu same as you did for the 50$ state. Now notice that the chance of getting broke increased to 67% and reaching 75$ probability came down to 33%.
Step 6: Modifying / Refining the model
Once you have completed the wizard step-by-step user interface for creating your Markov model, you will see the decision tree showing the Markov Process Diagram. Now, you can change the States, Transition Probabilities, Rewards, anything or everything. Please learn how to work on the diagram for modification from this page.