Value of Information
What is the "Value of Information"?
Say, you are in a market, shopping for an item. You know that if you drive to another market which is 10km away from where you are shopping, you may find the item either cheaper or more expensive. But at the same time, you need to count the cost of fuel to go and check out. So, unless the probability of getting the item for a low price is very high, or unless there is a possibility of getting the item for a very low price, you may not attempt to drive to the other market, right? Say, one of your friends is already in the market 2 and he called you over the phone and offered you to tell the price of the item from that market for a fee. What will be a good price for that information? Of course, you won't pay him higher than the most money you can save by shopping at market 2, right? That "correct fee for the price information that you will pay your friend" will be the value of the information. Value of Information is a number (usually in terms of money or utility) that you will find worth paying to get information that can help you to take a decision.
Expected Value of Perfect Information
Expected Value of Perfect Information is a number that can tell you, on average, what is the right price for Perfect Information about an uncertainty, if offered to you, you will find it worth paying to buy that information.
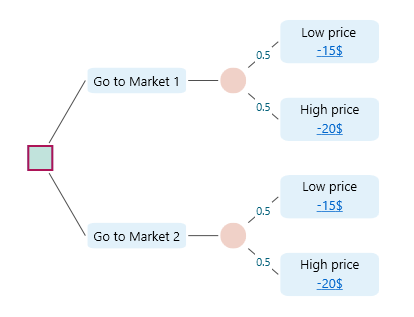
Let's revisit the shopping market example. Say, you want to buy an item which can be 15$ or 20$ in Market 1 and 15$ or 20$ in MArket 2. You do not know which market has 15$ and which market has 20$. Just assume 50% chances in both cases for both stores.
Markets are far away. Now, you are thinking, will it be worth driving to both of the markets to find out the price? If you know the price from both markets, on average, how much you can save? The amount of money that you could save on average just by knowing the prices from both markets, is called the "Expected Value of Perfect Information".
Calculation of Expected Value of Perfect Information
Let's calculate the Expected Value of Perfect Information for the above decision tree. Once we demonstrate the calculation steps, the concept of the value of information will be much clear. So, let's do it.
The expected value of the cost in Market 1 = 0.5 * 15 + 0.5 * 20 = 17.5
The expected value of the cost in Market 2 = 0.5 * 15 + 0.5 * 20 = 17.5
The lowest of the Expected Values from both markets is = Minimum of (17.5, 17.5) = 17.5
So, without any information, on average, you will spend 17.5$ to buy that item, if you randomly choose any market.
Let's call this value "Expected Value Without Perfect Information" or 'EVwoPI'. Cause, we do not have the perfect information yet about which market costs that item for what price.
Now, say, if you drive to both markets and check the price, then you will have perfect information about the prices in both markets. But, how can we measure the value of that perfect information before we know the perfect information? It will be easy if we think like this: Say, your friend has actually been in both markets and he knows the prices from both markets for that item. He is asking for some money to sell you that information. So, you are thinking, well, my friend, I do not know what exactly the information you got, but, I can tell that your information must match one of the following cases, right?
Case 1: Market 1 price: 15$, and Market 2 price 15$
Case 2: Market 1 price: 15$, and Market 2 price 20$
Case 3: Market 1 price: 20$, and Market 2 price 15$
Case 4: Market 1 price: 20$ and Market 2 price 20$
So, 3 out of 4 cases will let you buy the item for 15$, and 1 out of 4 cases will make you pay 20$ for the item.
If Case 1, Case 2, or Case 3 is true, you will be able to pick the market that offers the item for 15$ but if case 4 is true, then you will have to choose any market as both markets will ask you to pay 20$.
So, 75% chance that you will pay 15$ and a 25% chance that you will pay 20$. So, you can calculate a weighted average of the value of that Perfect Information even without really getting the information.
The Expected Value with Perfect Information = 0.75 * 15 + 0.25 * 20 = 16.25
So, if you get that perfect information, on average, you may spend 16.25$ for the item.
See, your friend did not hand over the Perfect information yet, but, for you, based on 4 possible cases, you can calculate the value of the information he is hiding from you.
So, you are thinking, how worth is the Perfect Information your friend is hiding from you?
Notice that, without the Perfect Information, you were about to spend 17.5$ on average if you choose any random market. Now, with the perfect information, that average cost came down to 16.25$.
So, actually, on average, how much was the saving with the perfect information?
The saving was : 17.5$ - 16.25$ = 1.25$
This is our Expected Value of Perfect Information for this decision scenario. You should not pay your friend more than 1.25$ for the price information. If your friend offers you the information for less than 1.25$, then it will be worth buying that information.
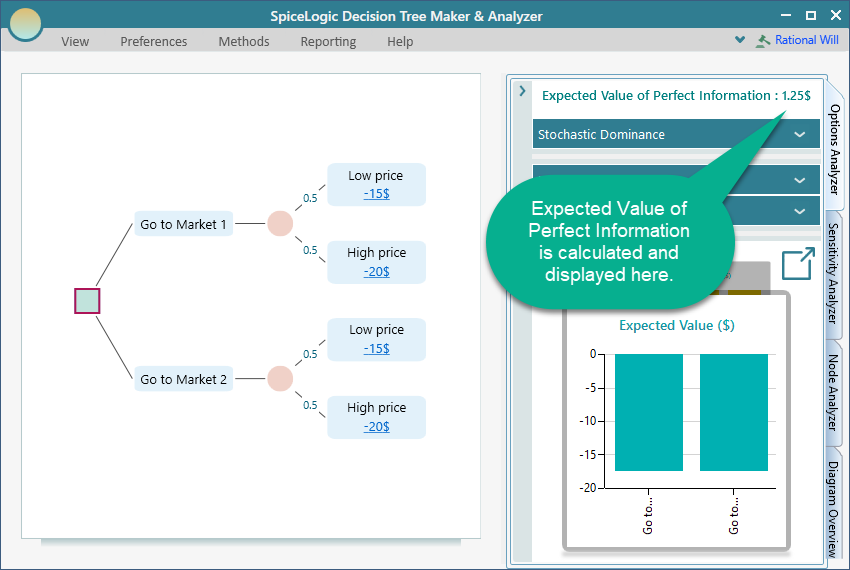
EVPI in the Decision Tree Software
The SpiceLogic Decision Tree Maker and Analyzer will calculate the Expected Value of Perfect Information for a decision tree automatically. After you make a decision tree, simply look into the "Options Analyzer" tab as shown below. If there is any uncertainty in the Decision Tree, then the Options Analyzer will calculate and display the Expected Value of Perfect Information for you. Notice that, the Expected Value of Perfect Information is calculated as 1.25$ which matches our hand calculation for the given decision tree.