Global Events and Decision Matrix

We have explained how to Modeling Uncertainty in a decision matrix. Say, you are thinking about 2 alternatives where outcomes are uncertain. The uncertain events are applicable to both alternatives. For example, you are planning to go to school for a diploma or take a job offer at hand. If you go to school for diploma and finish the program, your chance of getting a higher salary will increase. But, you are afraid that, within the next few years, there can be a recession and getting a job will be kind of impossible. So, should you take the risk of turning down the job offer and go to school or not?

Notice that, the Recession event is applicable to both alternatives. We can call this event a global event. That means, the event is global to both options.

Let's see how you can model such uncertainty.

Start the Decision Matrix and create an objective "Maximize Salary" as a Number type. We have demonstrated how to model objective in the Getting Started to Decision Matrix tutorial.

Say, your job offer at hand will give you 90,000$/year. But if you finish the diploma and get a job, you expect to get a salary of 120,000$/year.

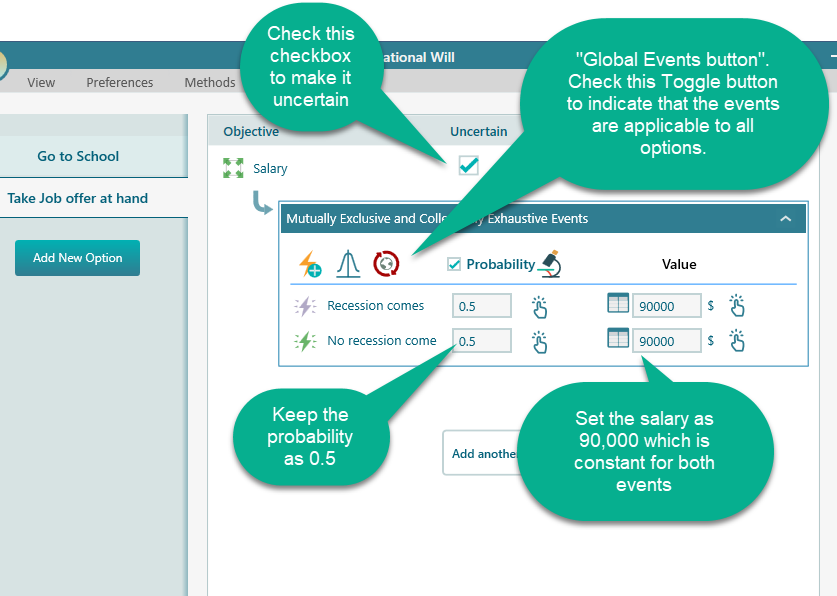
Say, the chance of recession is unknown, so let's keep its probability as 0.5.

Model the option "Take job offer at hand" as shown below. Notice the Global event button. Click that button to make the events global ("applicable to all options")

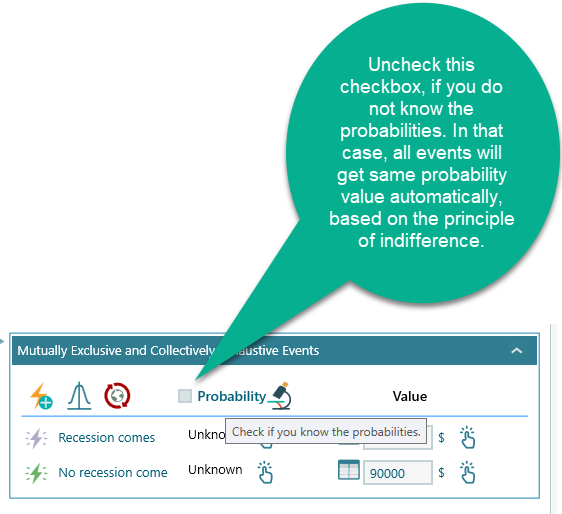
If you do not know the probabilities of the events, you can take the benefit of the "Principle of Indifference". According to the principle of indifference, when the probabilities are unknown, all events are assigned to equal probabilities. So, you do not have to enter 0.5 manually. Say, if you add another event, then all event will get probability = 1/3.

Anyway, now, select the option "Go to School". You will see the same global events are created for that option as well because you checked the global event button. If the recession comes, then your salary will be 0, because you won't have a job. But if the recession does not come, then your salary can be 120,000. Model this scenario as shown in the following screenshot.

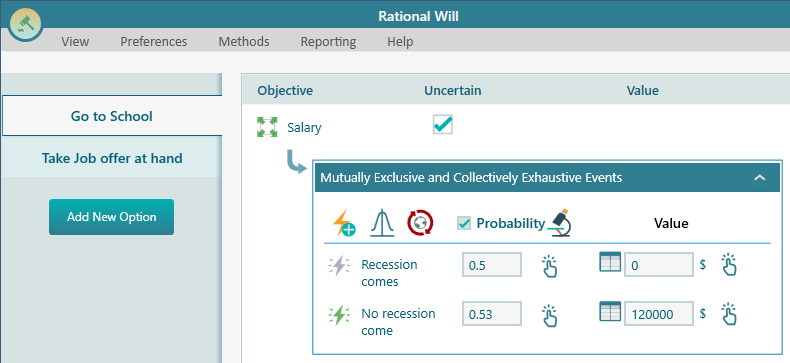
Now, you are done modeling the situation. Let's analyze the result.

Analyzing the Result

Expand the Options analyzer and you will see the following calculated insights.

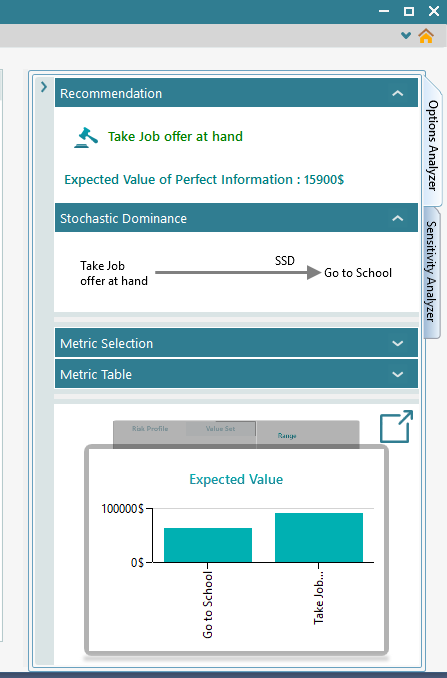
Notice the recommendation is made based on "Maximize Expected Value" criteria. You can see the Expected value chart. Notice that the expected value of "taking the job offer at hand" has higher expected value. Also "taking the job offer" option dominates the "Go to school" option by Second Order Stochastic Dominance. The expected value of perfect information is also calculated.

Sensitivity Analysis

Of course, a decision analysis is not complete until you have performed a sensitivity analysis. You want to know, which factor is actually the driving factor in this decision. Let's see that. Expand the "Sensitivity Analysis" tab.

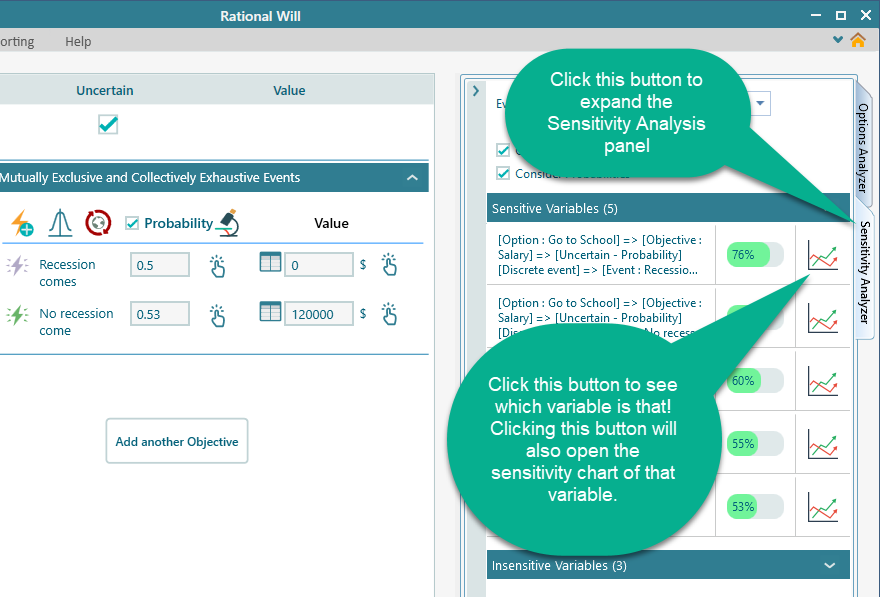
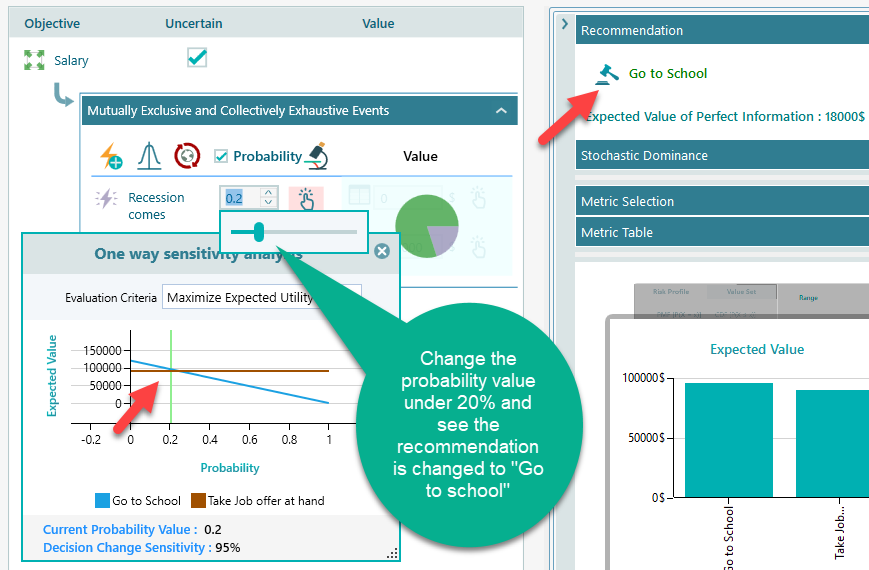
From the Sensitivity analysis tab, we can see the most affecting variable is 76% sensitivity. It gives you a clue about the variable.

Once you click that button, you will see the following view.

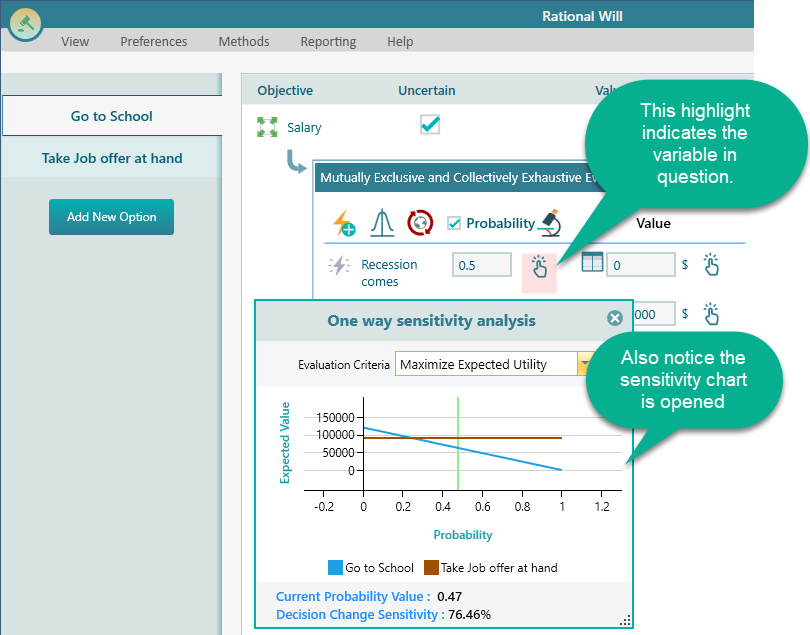
From the above chart, you can clearly understand that the probability of recession is the main factor in this decision. If the probability was very low, then of course, going to the school would be the most rational choice. But if the probability of recession is high, then taking the job offer at hand would be the right choice.