Consistency ratio and Transitivity Rule
The consistency ratio is a metric that indicates the consistency between pairwise comparisons. Suppose you like an apple twice as much as an orange
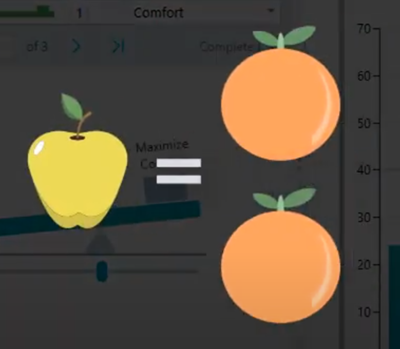
And say, you like an orange 3 times as much as a banana.
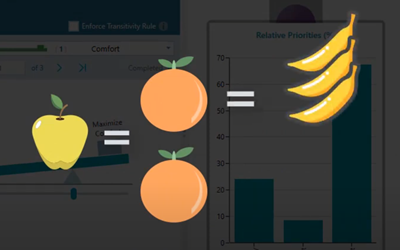
Logically, you should like an apple 6 times as much as a banana.

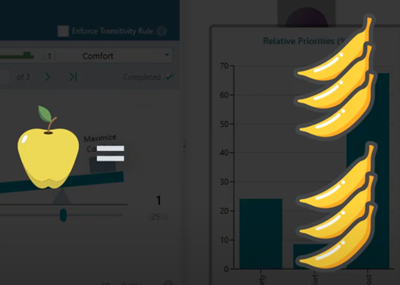
When you are presented to compare Apple and banana, and if you do not like apple 6 times as much as a banana, then obviously there is an inconsistency in your preference.
Consistency ratio measures that inconsistency. It is a measurement that indicates how much you deviate from the consistency. When you are 100% consistent in your preferences, the deviation will be 0. The higher is this
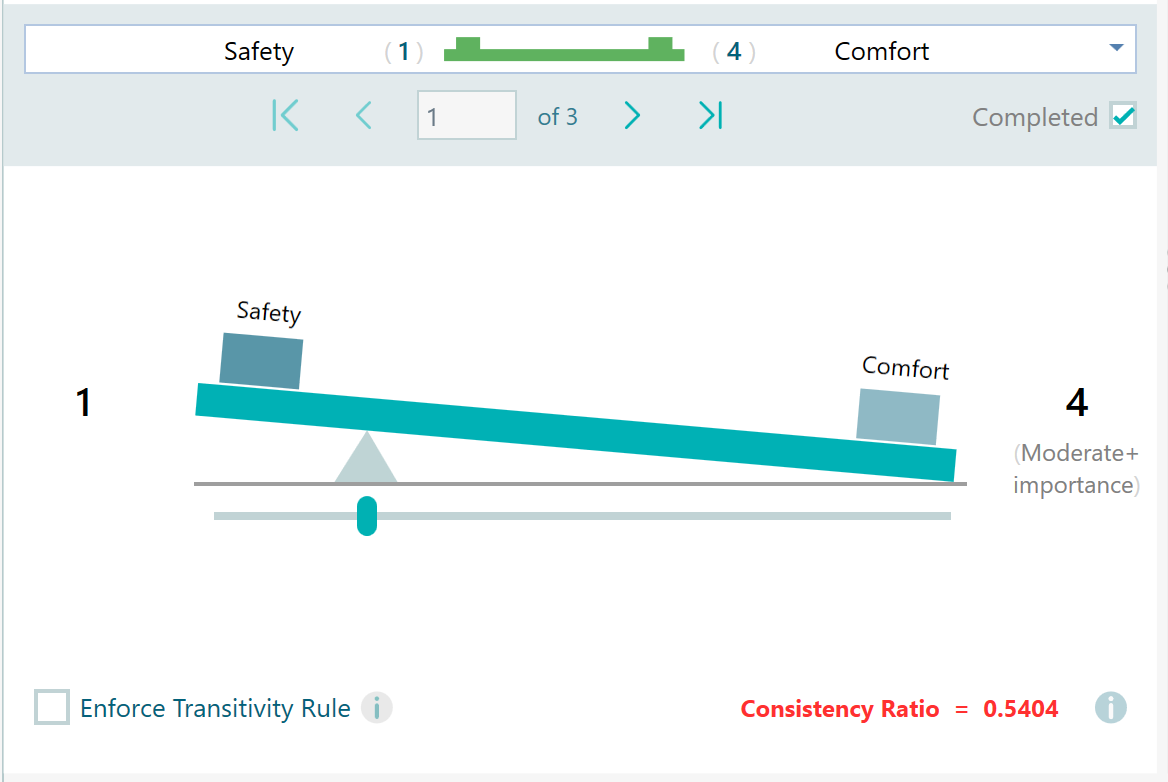
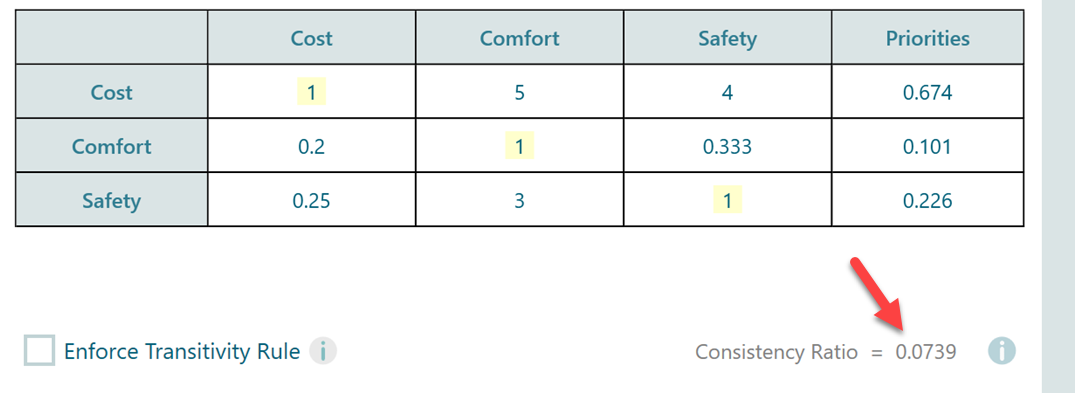
In the SpiceLogic ahp-software, whenever you perform a pairwise comparison or view the pairwise comparison matrix, you will notice the consistency ratio for that set of comparisons calculated and displayed at the bottom as shown below.
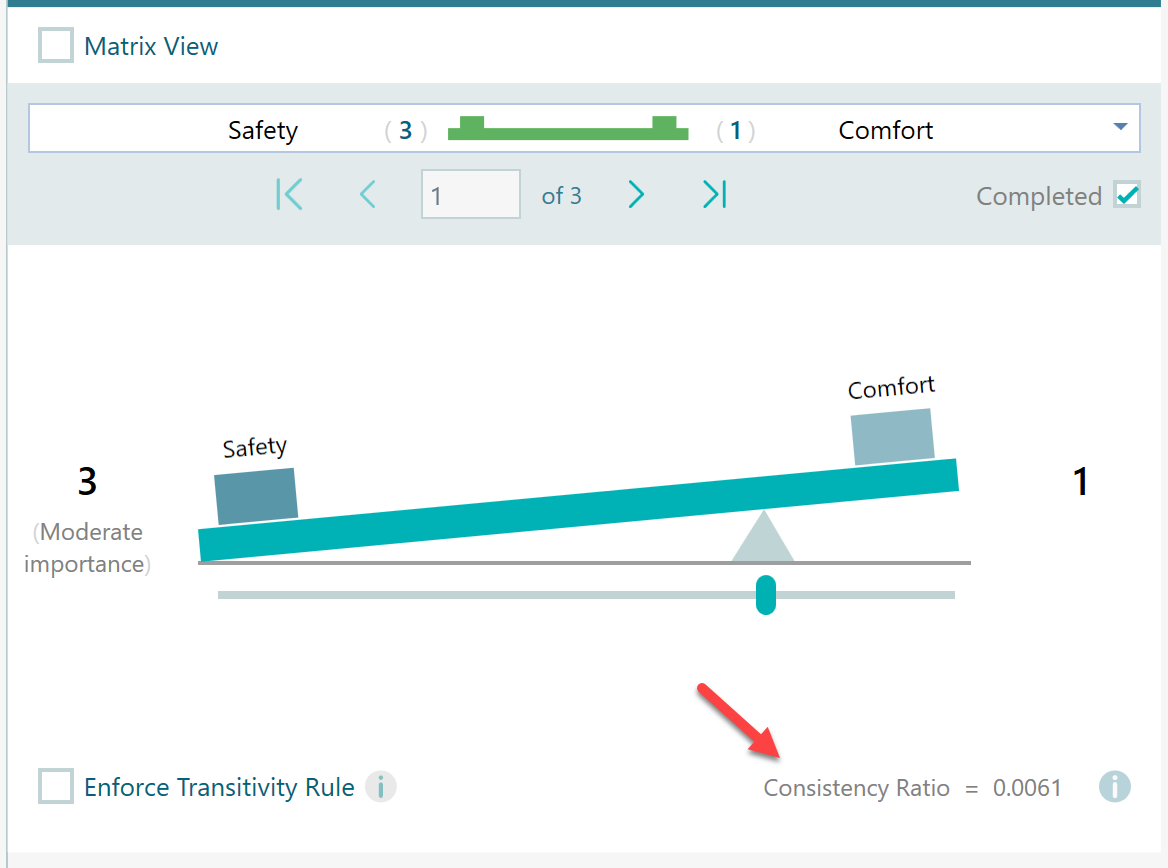
According to Thomas L. Saaty, the consistency ratio should be less or equal to 0.1. So, if your consistency ratio is not less or equal to 0.1, then it is necessary to revise your judgments. If your Consistency ratio goes over 0.1, the software will indicate that using a Red bold color, as you can see on this screen.
Calculation method
First, you learned how the pairwise comparison priorities are calculated from this page.
Once the priority vector is calculated, we get the Principal Eigen Value from the pairwise comparison matrix. Then, based on the Principal Eigen Value, we calculate the Consistency Index metric. And finally, from the Consistency Index metric, we calculate the Consistency Ratio.
Say, we have a pairwise comparison matrix as shown below.
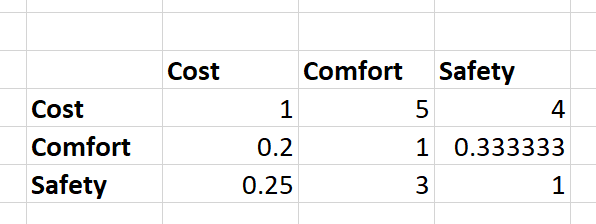
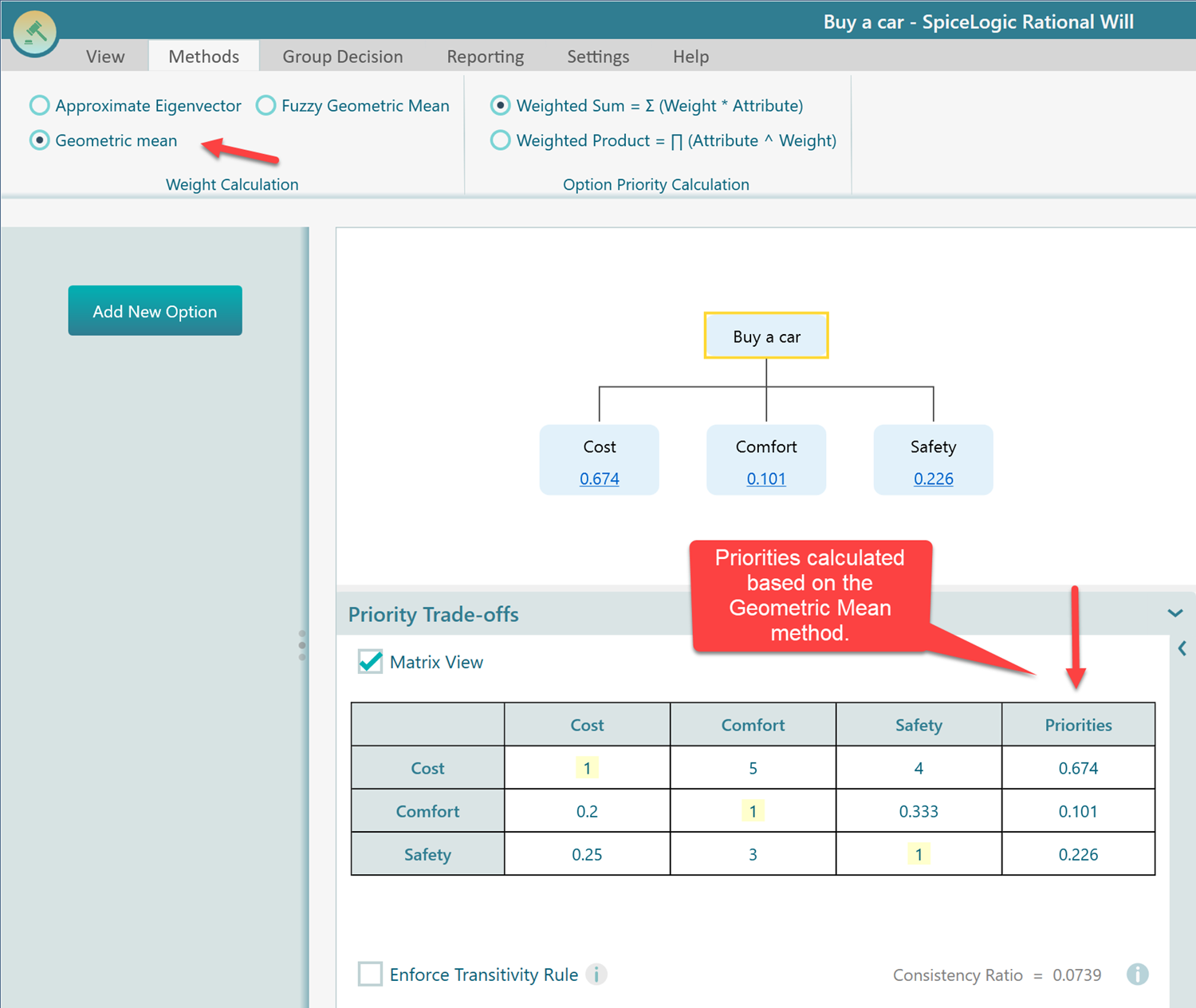
Say, based on the geometric mean method, we got the following priority vector.
Now, in order to get the Principal Eigenvalue, we perform a Matrix multiplication, the Pairwise comparison matrix X priority vector.
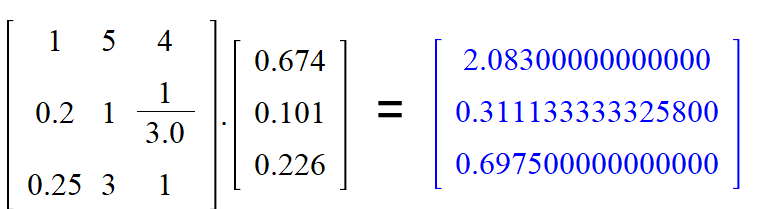
Then, from this multiplication result, we calculate the Eigen Vector like this. We divide a cell value of the matrix multiplication result vector by the corresponding priority vector cell.

Then, the principal Eigen Value is obtained by the average of this resulting vector, which is (3.090504451 + 3.080528052 + 3.086283186)/3 = 3.085771896.
The next step is to find the Consistency Index. The formula for the consistency index is
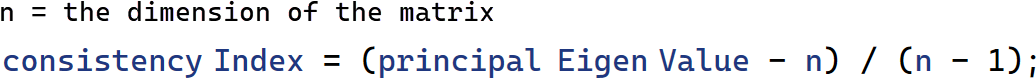
In our case, n = 3, and the principal eigenvalue is 3.085771896. So, we get the consistency index as 0.042885948
Now is the tricky part. AHP calculates a consistency ratio comparing the consistency index of the matrix versus the consistency index of a random matrix. A random matrix is a matrix where the judgments have been entered randomly. Therefore it is expected to be highly inconsistent. Thomas L. Saaty provided the calculated Random-like matrix value for matrixes of different sizes.

In our case, the number of items is 3 in the matrix, and therefore, our Random Index is 0.58.
We already got the consistency index as 0.042885948
Consistency Ratio = Consistency Index / Random Index.
= 0.042885948 / 0.58 = 0.0739.
Notice that, our SpiceLogic AHP Software displayed this Consistency Ratio of 0.0739 which matches the number that we got by our hand calculation.
Transitivity Rule
The transitivity rule is just another way of saying that, you must be consistent in your judgment. That means if this rule is applied, then, if you like an apple 2 times as much as you like an orange and if you like a banana 3 times as much as you like an orange, then, according to the transitivity rule, you must like a banana 6 times as you like an apple. If the transitivity rule is applied, then you are not allowed to choose a different comparison for apple and banana. The human mind may not follow the transitivity rule. That means, even though if someone chooses an apple 2 times as he likes an orange and if he likes an orange 3 times as he likes a banana, when he is presented to compare apple and banana, he may choose a different number, like 4 or 5 or something else. And that's why, in AHP, we ask the user to compare apple and banana as well even though he already compared apple vs orange and orange vs banana. But, think about it. If you enforce a transitivity rule, then, if you compare apple vs orange and orange vs banana, you do not need to compare apple vs banana because logically it can be inferred. In that way, we can reduce the number of pairwise comparisons. If you have a lot of criteria/sub-criteria in your analytic hierarchy process model, then the number of pairwise comparisons can be calculated as ½ * n * (n -1).
But, if you enforce the transitivity rule, then the number of pairwise comparisons can be reduced to simply (n -1).
It is a huge time saver indeed.
SpiceLogic Analytic Hierarchy Process software (a.k.a ahp-software) can let you enforce the Transitivity rule. Here is a screenshot showing how to enforce the transitivity rule.
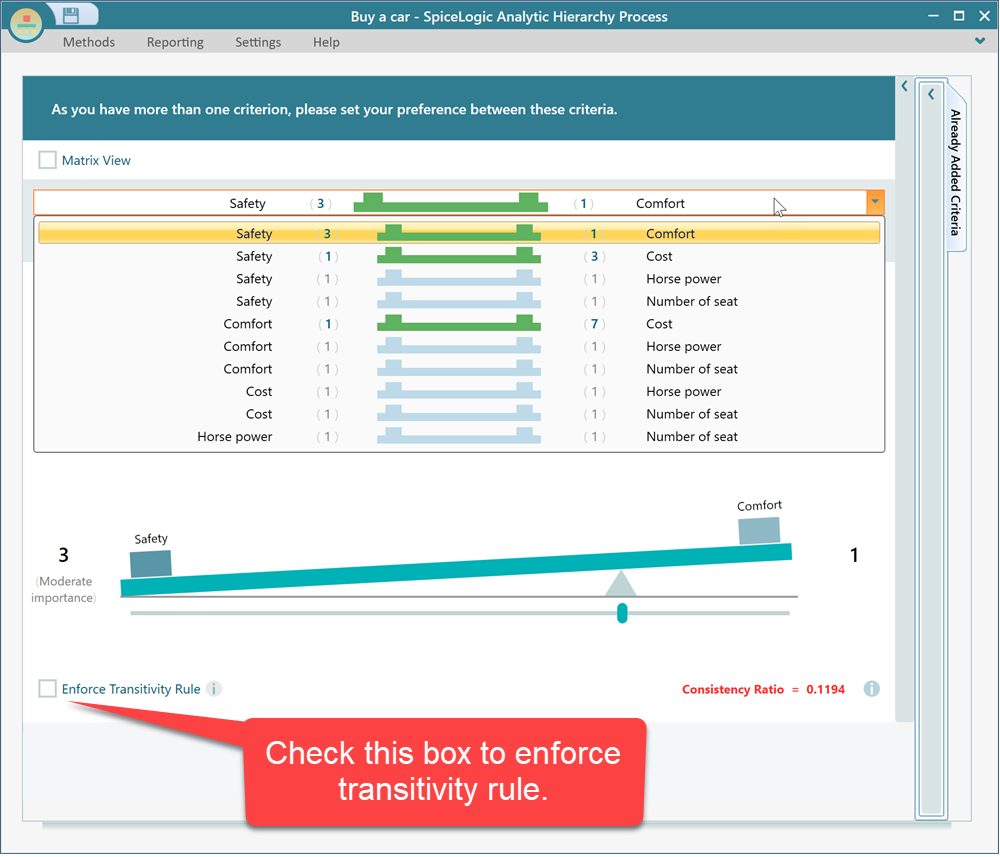
Notice that, before applying the transitivity rule, in the above screenshot, the number of pairwise comparisons is 10.
Now, after checking that checkbox, the number of pairwise comparisons has been reduced to 4.
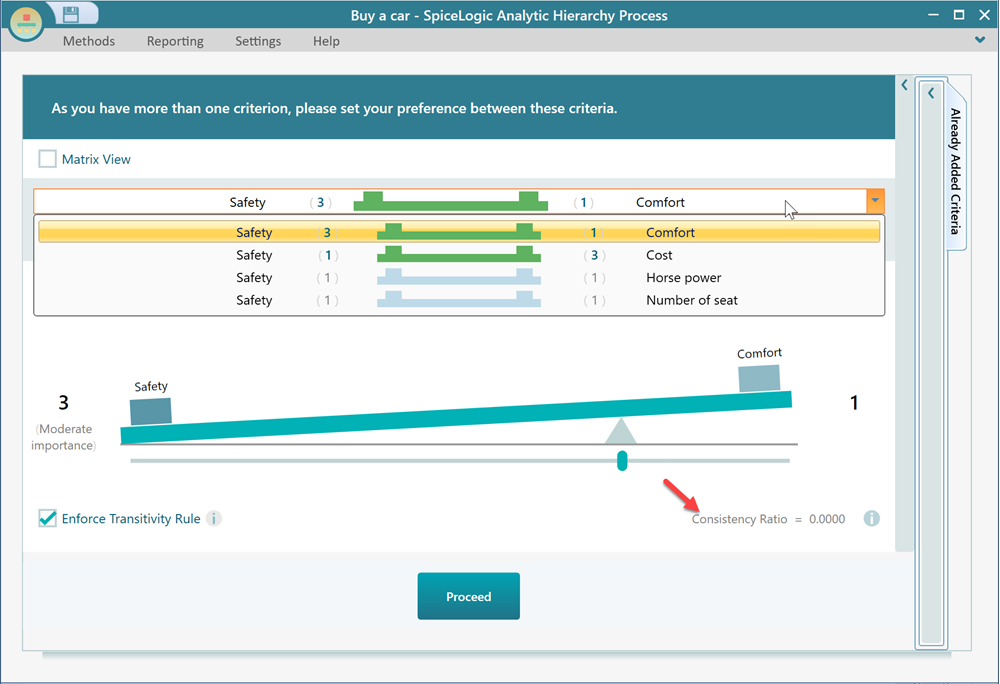
Also, notice that the consistency ratio metric is shown as 0. Naturally, as you are not allowed to make inconsistent judgments when the transitivity rule is applied, the consistency ratio will be 0, and that makes sense.