Calculation Methods
When you have specified your pairwise comparisons for criteria or options, a relative weight for each factor (criterion or option) needs to be calculated. Once the relative weight for that factor is calculated, that relative weight can be used to calculate the final weighted sum or weighted product for an option. In order to do that, there are various calculation methods can be chosen in the SpiceLogic AHP Software.
If you are in rush and worried about which method to choose, then, do not worry. Do not change any methods from this panel and continue using the default selected method. Because the default selected methods are regular standard and recommended methods. The other methods are provided to you just in case you find a reason to choose another method for experimentation. In our experience, we found none of these methods make a dramatic change in results. You will find that, no matter what method you choose, the result numbers stay almost the same and in very rare cases you may find the result decision changed just because you changed a calculation method. But, it is up to you if you would like to experiment with various methods for your specific problem model.
Approximate Eigen Vector method
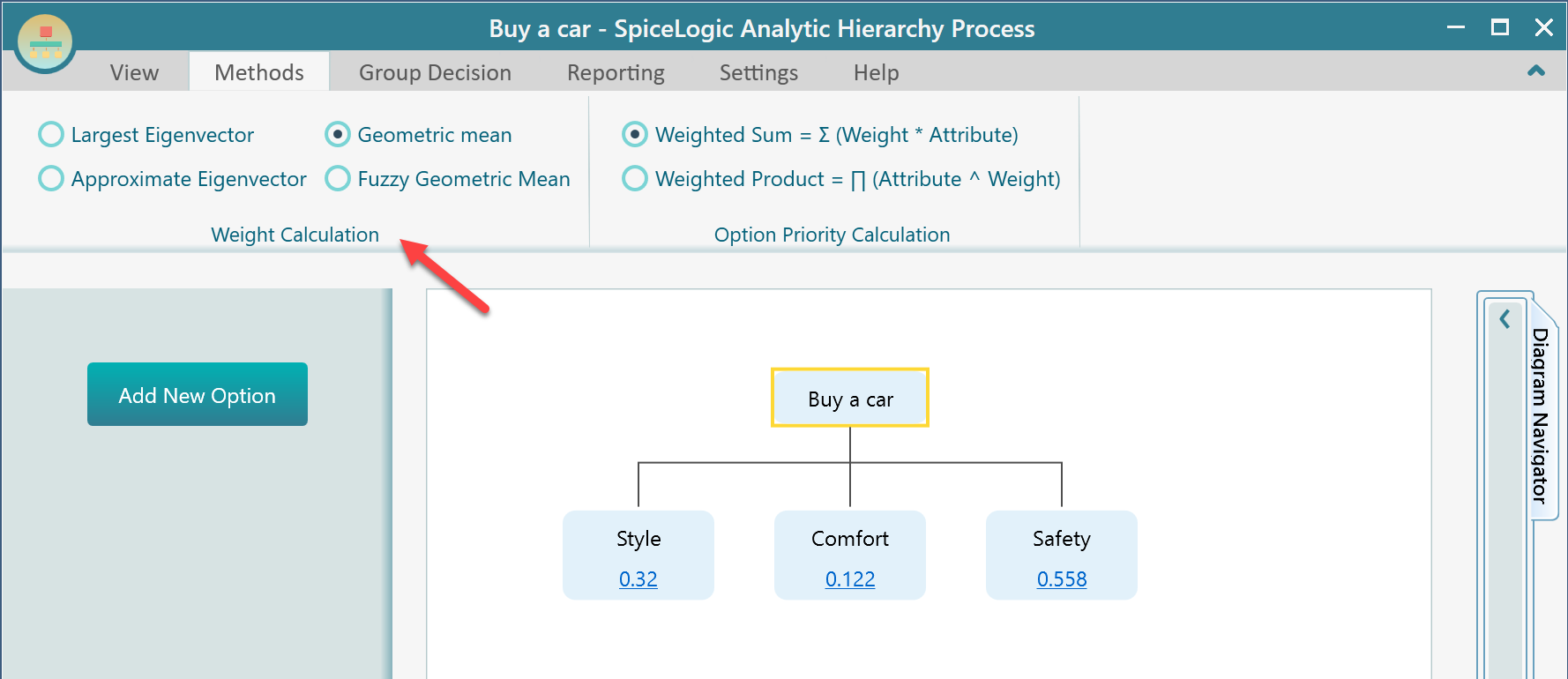
By default, you will find that the Approximate Eigen Vector method is chosen, and that method is recommended unless you have any specific reason to choose a different one.
This method is very simple to demonstrate. This method provides a valid approximation to the overall weights only when the comparison matrix has a very low inconsistency.
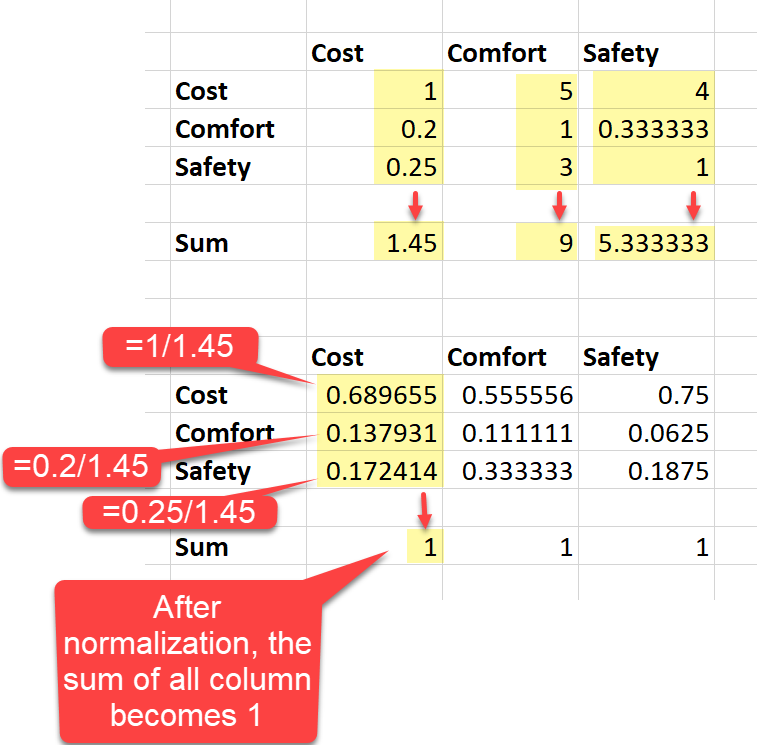
Step 1: Normalize the columns.
Say, we have a pairwise comparison matrix like this:
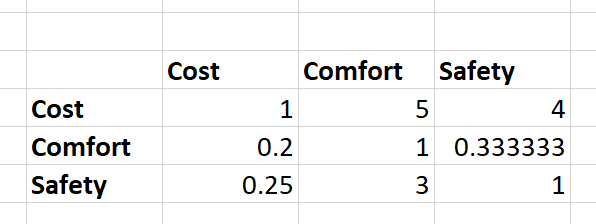
We need to normalize the columns so that the sum of all column values becomes 1. We do so by first calculating the sum of a column's cell values and then dividing each cell value of that column by that sum. Please check the following graphical demonstration of this process.
Step 2: Taking the arithmetic mean of the row
From this normalized matrix, we can obtain the overall or final priorities by calculating the arithmetic mean of each row.
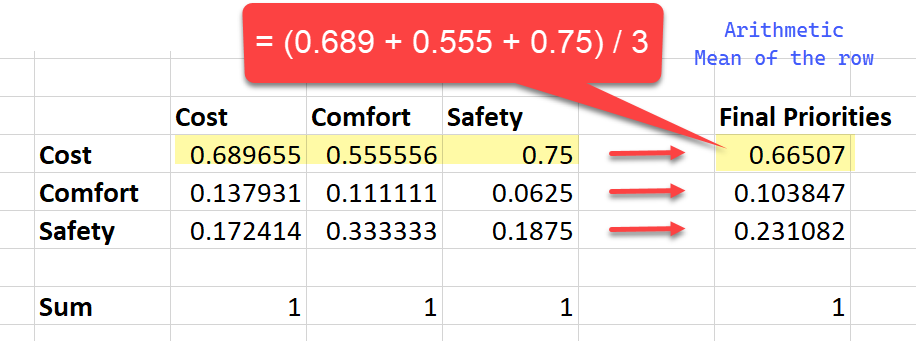
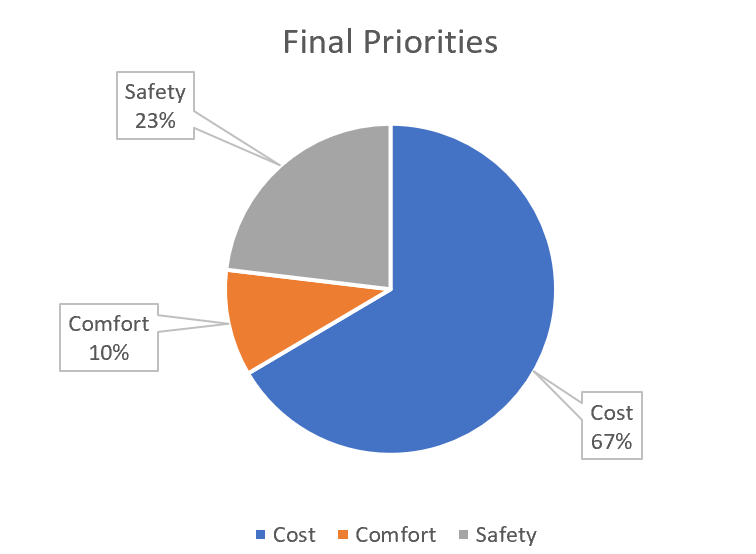
This is how the priorities are calculated in the SpiceLogic AHP Software when you choose the Approximate Eigen Vector method, as you can see from the screenshot.
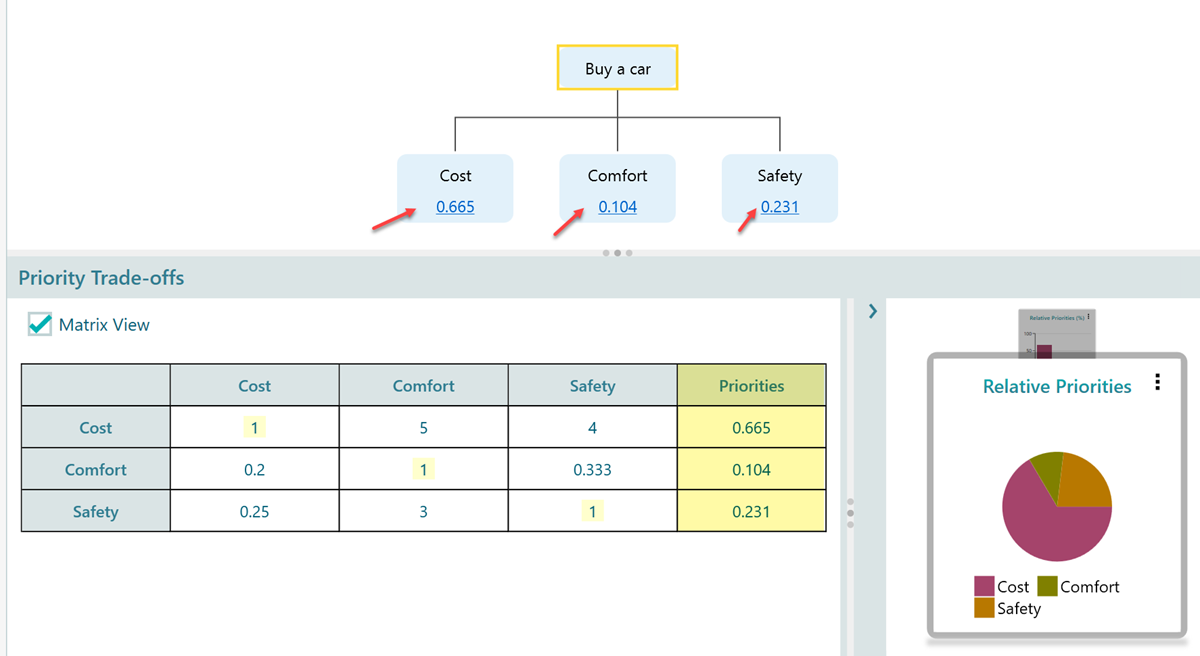
Largest Eigenvector method
You can learn about this method from this article: https://medium.com/dlprodteam/the-ahp-pairwise-process-c639eadcbd0e
Geometric Mean method
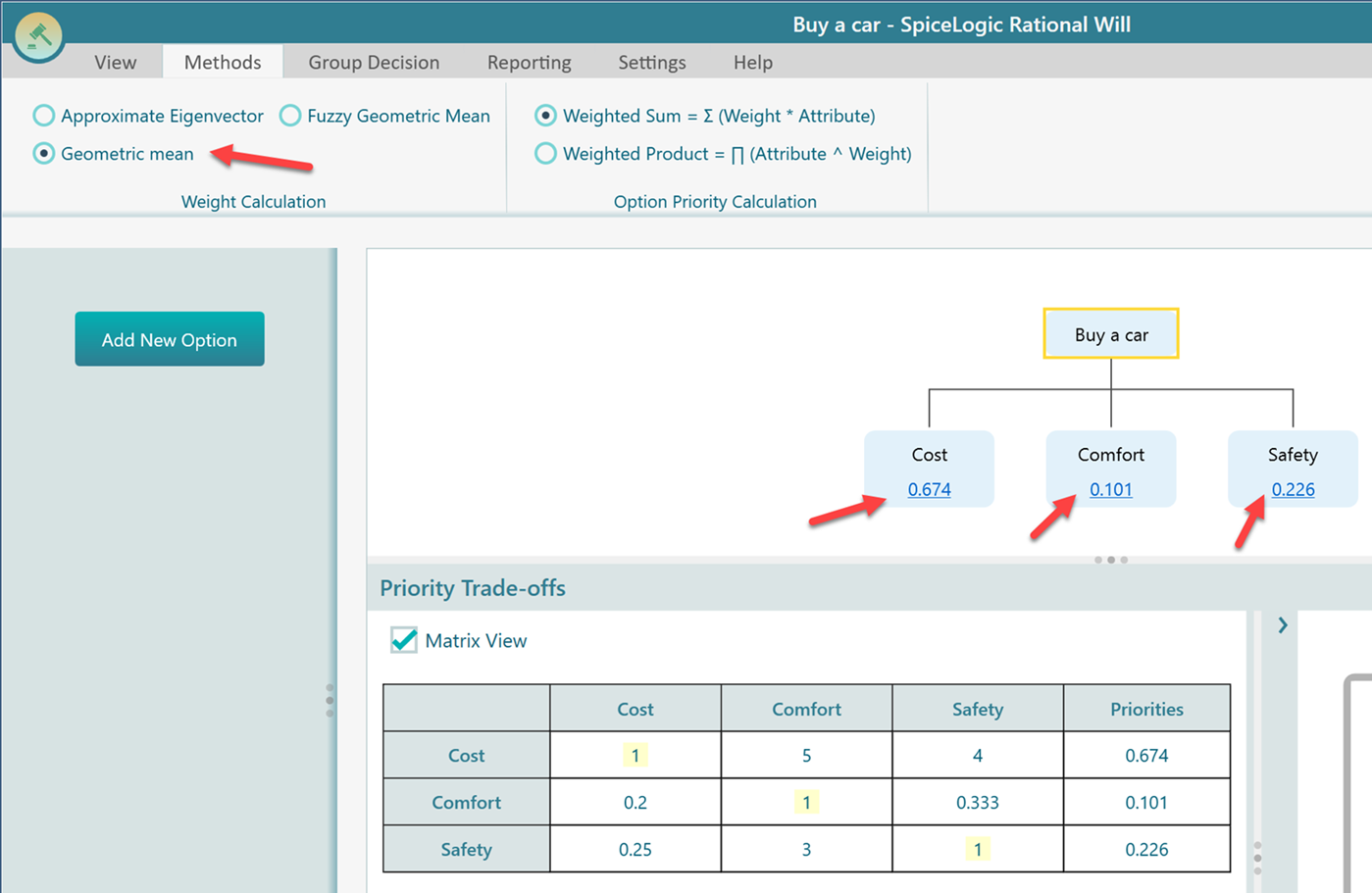
If you choose the geometric mean method, first, we calculate the geometric mean of a row in the pairwise comparison matrix. That geometric mean is the priority value of the factor indicated by the row. But, we also want that the sum of all priorities should be 1. So, we normalize the priorities by dividing each priority value by the sum of all priorities that we got from the geometric mean. This process is demonstrated in the following figure.
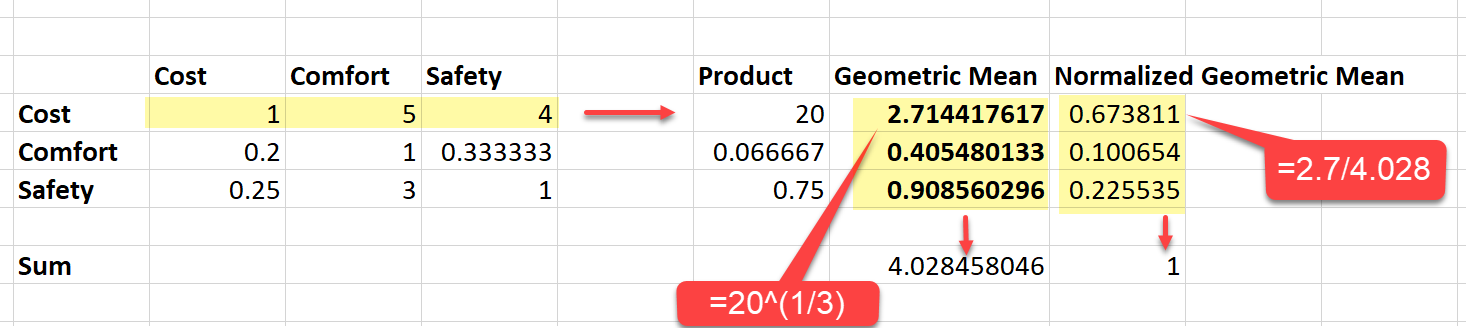
Let's explain the process in detail. The left side of the above figure shows the original pairwise comparison matrix. Consider the first row "Cost" and get the product of the values of this row. The product of the values is 1 x 5 x 4 = 20. The geometric mean is the 3rd root of this product, which can be indicated by the symbol 20 ^ (1/3.0). In Excel, you will get it by the formula:
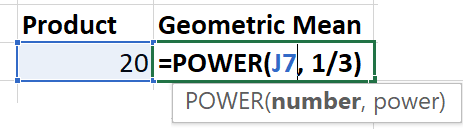
The geometric mean we get by calculating 20 ^ (1/3.0) = 2.71. So, the priority of "Cost" is 2.71 according to the geometric mean. In the same way, we get the geometric mean of the rest of the rows "Comfort" as 0.405 and "Safety" as 0.908. But, we also want to normalize the priorities so that the sum of all priorities becomes 1. In order to do that, we add up all priority values, (2.7144 + 0.405 + 0.908) = 4.028. Then, we divide each priority value by the number 4.028. In that way, we get the final priority value for "Cost" as 0.67, "Comfort" as 0.10, and "Safety" as 0.22.
Now, notice that, in the SpiceLogic AHP Software, when you chose geometric mean for this pairwise comparison matrix, the result shows up in the diagram and the table according to our hand calculation.
Fuzzy Geometric Mean Method
There is a YouTube video that we found best to explain the method we have adopted for calculating the fuzzy geometric mean for AHP. Here is the YouTube link: https://www.youtube.com/watch?v=5k3Wz1AfVWs
Calculating Consistency Ratio
In every pairwise comparison panel, you will notice that another metric is also shown, named "Consistency Ratio". If you want to know how we calculate the consistency ratio, please check this dedicated page for Consistency Ratio.
Calculating the Final Option Value
We have learned how to calculate the priorities from a pairwise comparison matrix. Based on a chosen strategy, we calculate the priorities of each criterion.
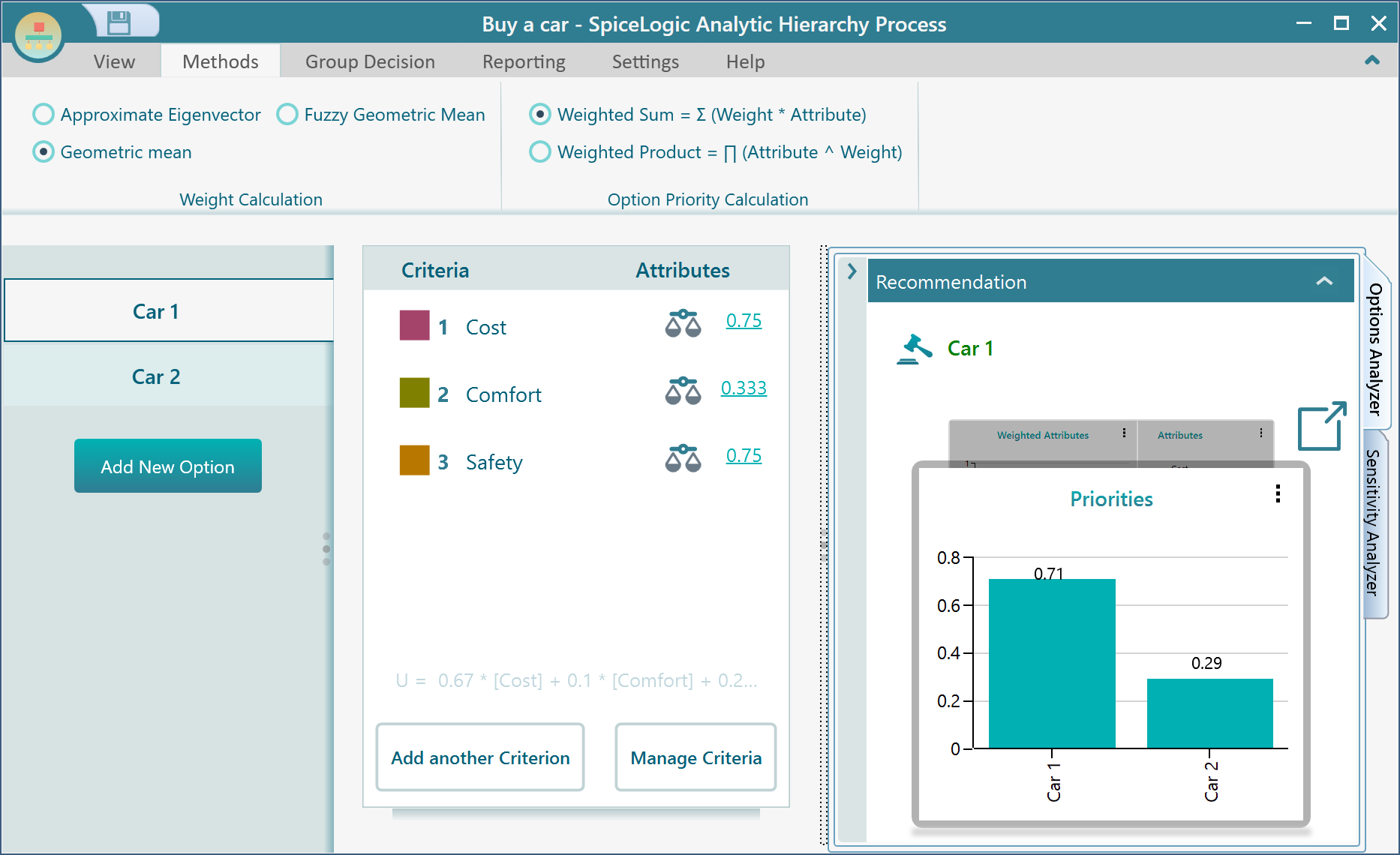
Say, we got the relative weight for Cost as 0.665. And also, say, we got two options, "Car 1" and "Car 2". Now, we perform a pairwise comparison of "Car 1" and "Car 2" against the criterion "Cost", and get a priority vector.
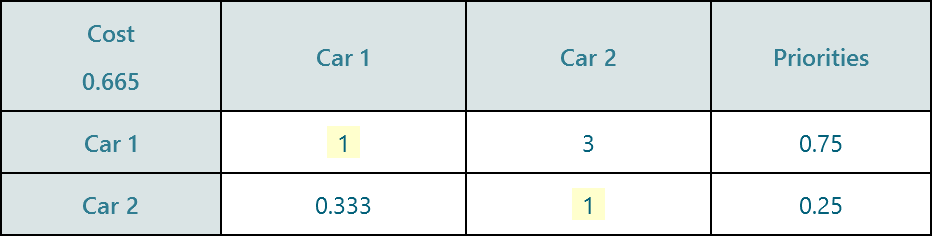
In the same way, we perform the pairwise comparison for all options against each criterion.
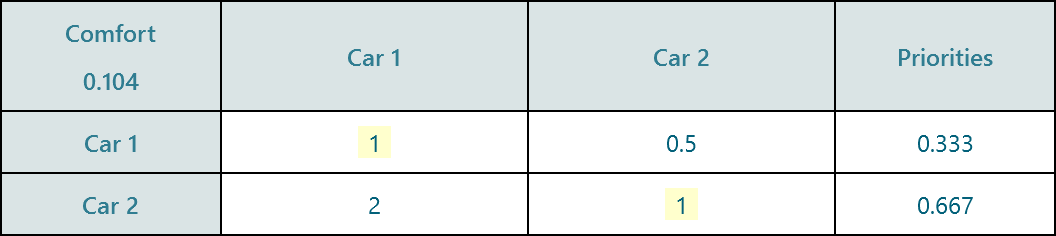
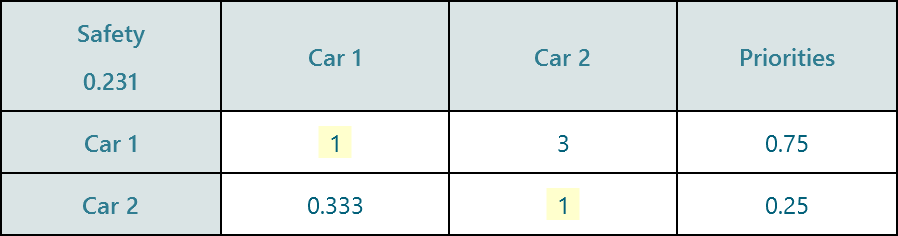
Then we calculate the weighted sum or weighted product to find out the final priority value of an option.
Notice that, after the pairwise comparisons, we got the attribute value for Car 1 as:
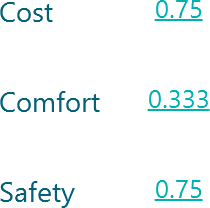
And Car 2 attributes as
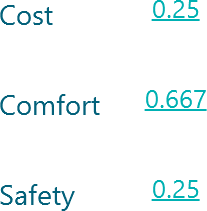
Now, we need to combine the attributes of the options to calculate the final value. We have two options to do so. One is the default option "Weighted Sum" and another option is "Weighted Product". By default, you will find the "Weighted Sum" method is selected. Because that is the regular recommended method. But, if you like to experiment about what if you choose Weighted Product, you can do that from this panel.
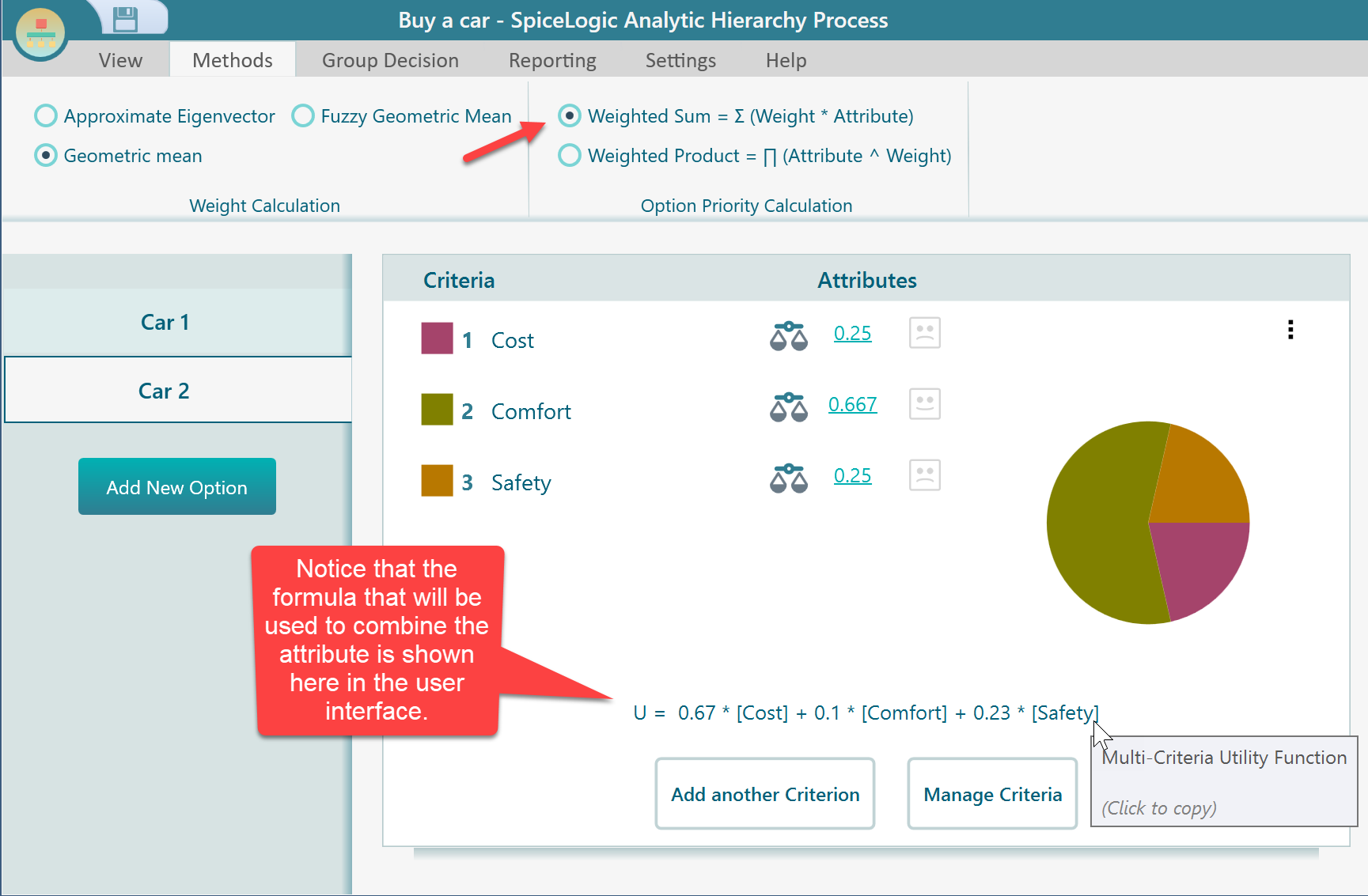
If you change the method to "Weighted Product", you will see the displayed formula changed as shown below.
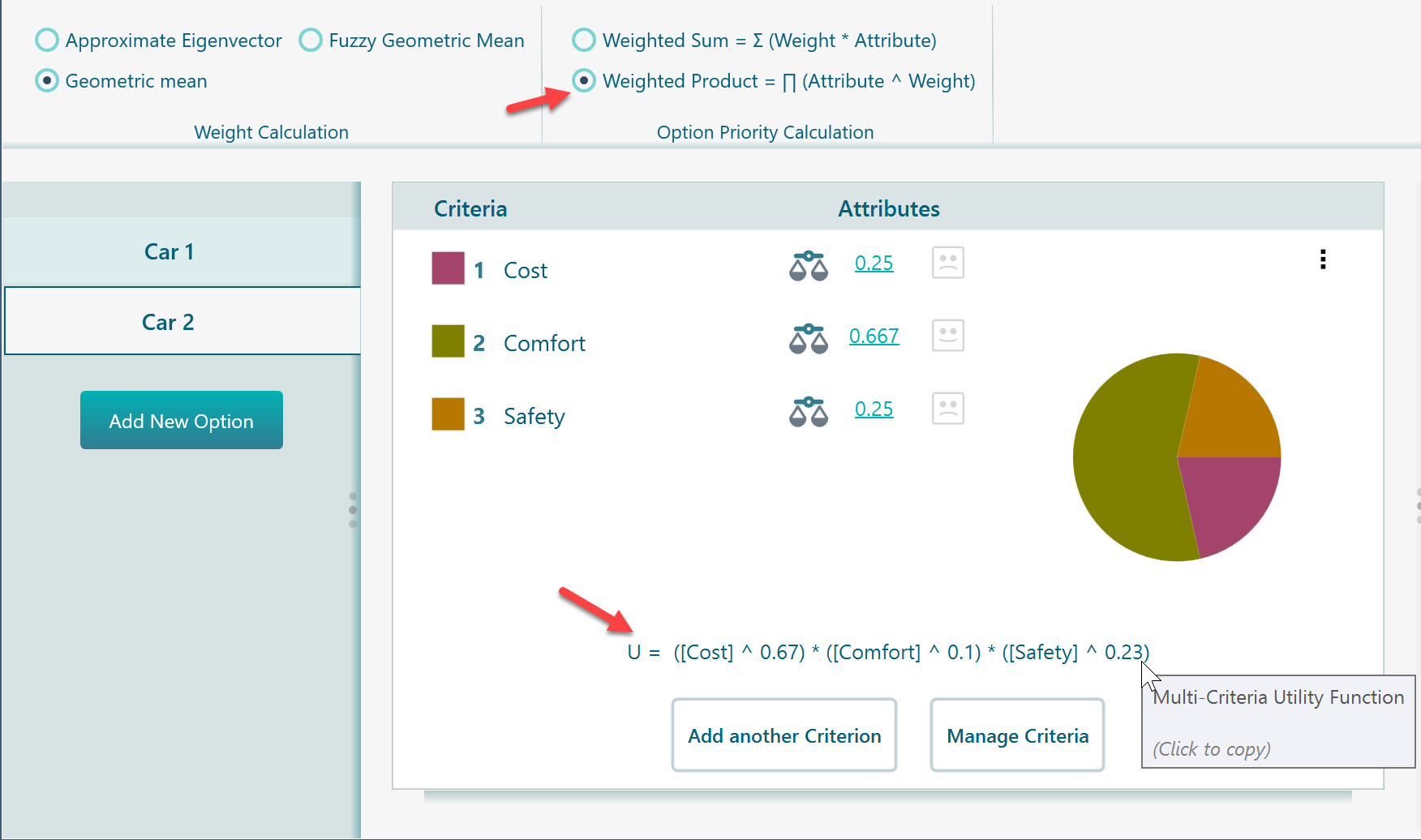
Say, you selected the Weighted Sum method, then, the following formula will be used to calculate the option value.
= [Weight of Cost factor] . [Cost attribute for Car 1] + [Weight of Comfort factor] . [Comfort attribute for Car 1] + [Weight of Safety factor] . [Safety attribute for Car 1]
Lets calculate the value for Car 1:
= (0.67 x 0.75) + (0.1 x 0.333) + (0.23 x 0.75)
= 0.71
Lets calculate the value for Car 2:
= (0.67 x 0.25) + (0.1 x 0.667) + (0.23 x 0.25)
= 0.29
As the Car 1 scores 0.71, higher than the Car 2 score 0.29, the AHP software recommends "Car 1" as you can see here.