Modeling Cumulative Distribution Function
The cumulative distribution function is a function that gives the probability of occurring something for AT MOST a number of times. It can be said another way: Mathematically (from Wikipedia),
The CDF of a continuous random variable X can be expressed as the integral of its probability density function ƒX as follows:
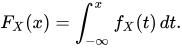
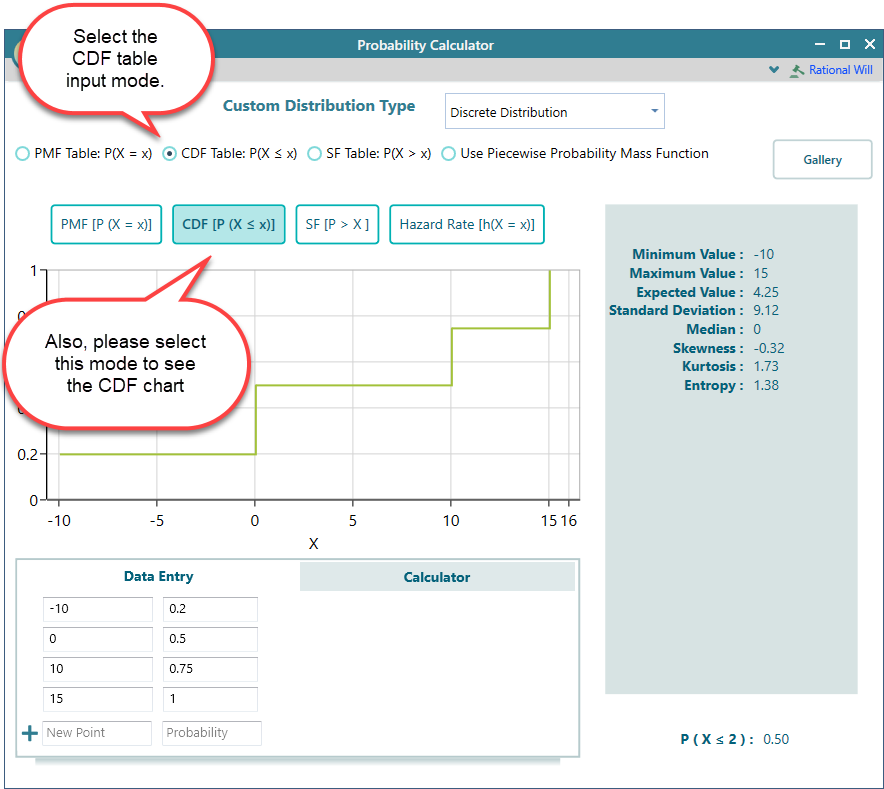
Your options are not limited to only Probability Mass Function or Survival function when using a data table for modeling a probability distribution.
You can prepare a table that represents the Cumulative Distribution Function of your desired probability distribution. Select the CDF table radio button as shown below:
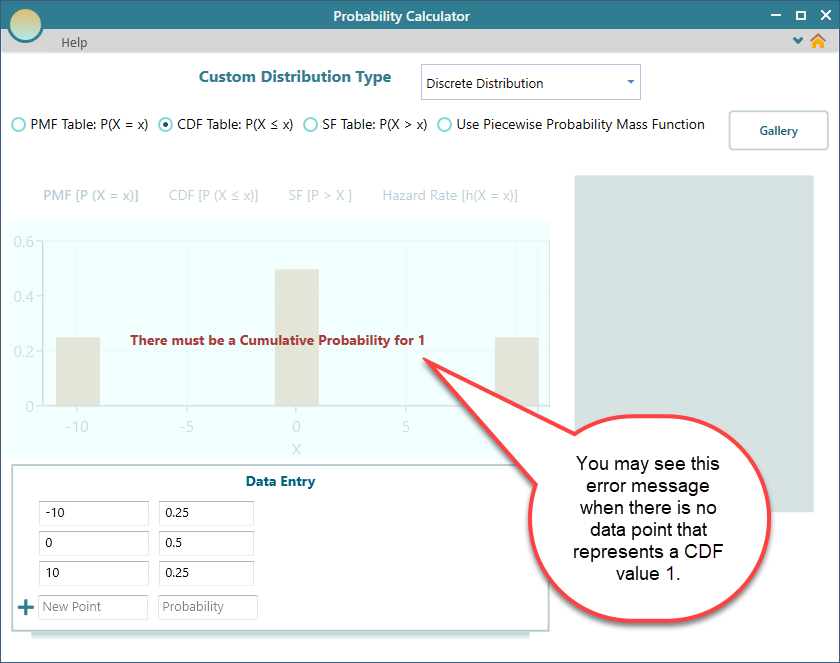
As you know, in a Cumulative Distribution function, there must be a random variable definition whose CDF value is 1. If you do not provide an entry for value = 1, you will see the error message "There must be a Cumulative Probability for 1". So, just fix the table by adding an entry for CDF value = 1.
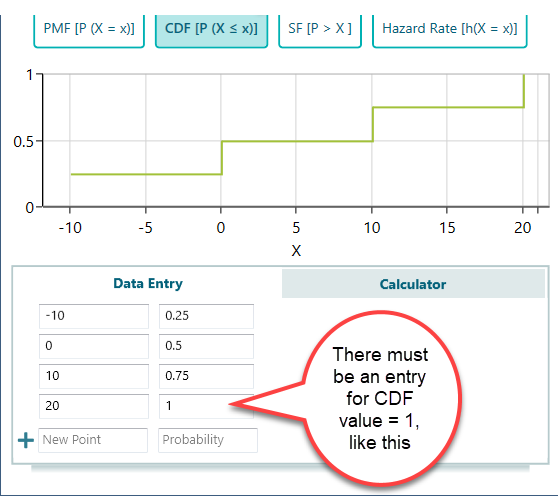
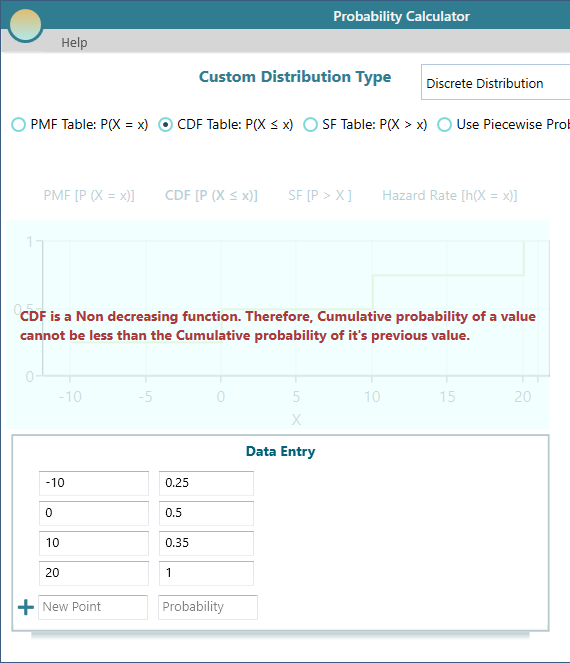
CDF is a Nondecreasing function.
A function f(x) is called non decreasing function, when, for any 2 values of x, say a, and b,
If a < b, then it must be true that, f(a) ≤ f(b)
Cumulative Distribution Function is a nondecreasing function. Therefore, in a CDF table, the CDF value for an entry must be equal to or higher than the CDF value of the previous row.
If you do not enter values in the CDF table according to this rule, then you will see an error message like this:
"CDF is a Nondecreasing function. Therefore, the cumulative probability of a value cannot be less than the Cumulative probability of its previous value."