Multiple-criteria decision analysis
When there is a complex problem, structuring well and considering multiple criteria explicitly leads to more informed and better decisions. In our daily lives, we usually weigh multiple criteria implicitly, and we accept the consequence of such decisions that are made based on only intuition. But when the stakes are high, it is essential to evaluate multiple criteria explicitly. Multiple-criteria decision analysis (MCDA) is a sub-discipline of operations research. This analysis model explicitly evaluates multiple conflicting criteria in decision-making. For example, cost or price is usually one of the main criteria, and quality is typically another criterion, easily in conflict with the cost.
This tutorial will elaborate on the following concepts of MCDA with the Decision Tree software.
Multiple Objectives in a Decision Tree
In a decision tree, the payoff depends on your objective. When you are looking for a new job or choosing a job offer from multiple offerings, you may have the following objectives:
- Maximize Salary
- Minimize Distance from Home
- Must be a Management Role
- Minimize the chance of Micro-Management
etc.
That means you have multiple objectives. So, when you make a decision tree and set a payoff to a node, you need to express the payoff in terms of objectives. Most quick decisions usually involve just one objective "Maximize profit" or "Minimize Cost." Therefore, the decisions are based on one single criterion "monetary gain". But for a quality decision, you need to define multiple objectives and set the payoff in terms of the criterion found from these objectives. The Decision Tree Software is modern featured software that allows you to model multiple objectives and let you express payoff in terms of multiple objectives as shown below.
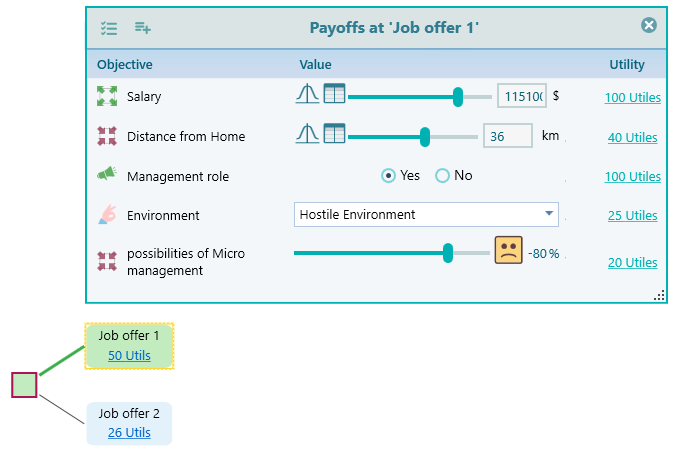
Criteria vs. Objectives
So what is the Criterion, and what is the objective? The criterion is kind of a scale where you can express your payoff in terms of that scale. For example, if you have an objective "Maximize Profit". Then your criterion is "Profit". When you set the payoff to a node, you will set how much profit you expect from an outcome in terms of dollars or other currency.
Decision Tree Software will let you define your objective easily using its intuitive user experience, and then it will extract the criterion from your objective and ask you to set a payoff for that criterion.
Setting up Criteria
When you start the Decision Tree Software, you are presented with the following screen.
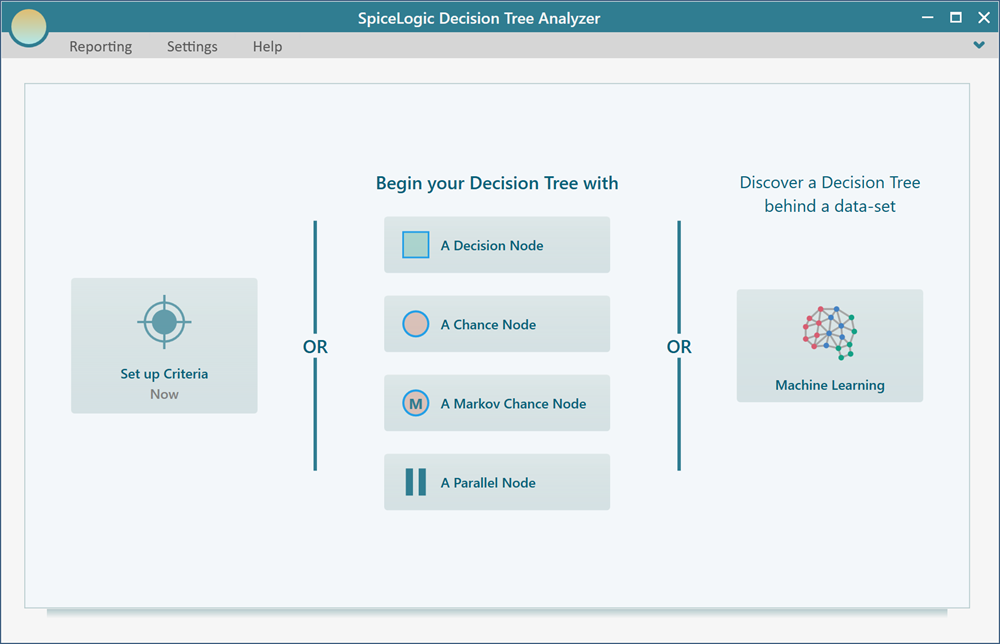
There are two ways to proceed from this start screen. You can start creating the decision tree immediately by clicking one of the buttons from the right side (i.e. Clicking the button "A decision node"). Or you can click the button "Set up Criteria" to set up the criteria first. If you create the decision tree first, then you can set up the criteria anytime by clicking the payoff button from the node.
If you click the button "Set up Criteria", then you will see the following screen. Click the first button "Regular single or multiple criteria..."
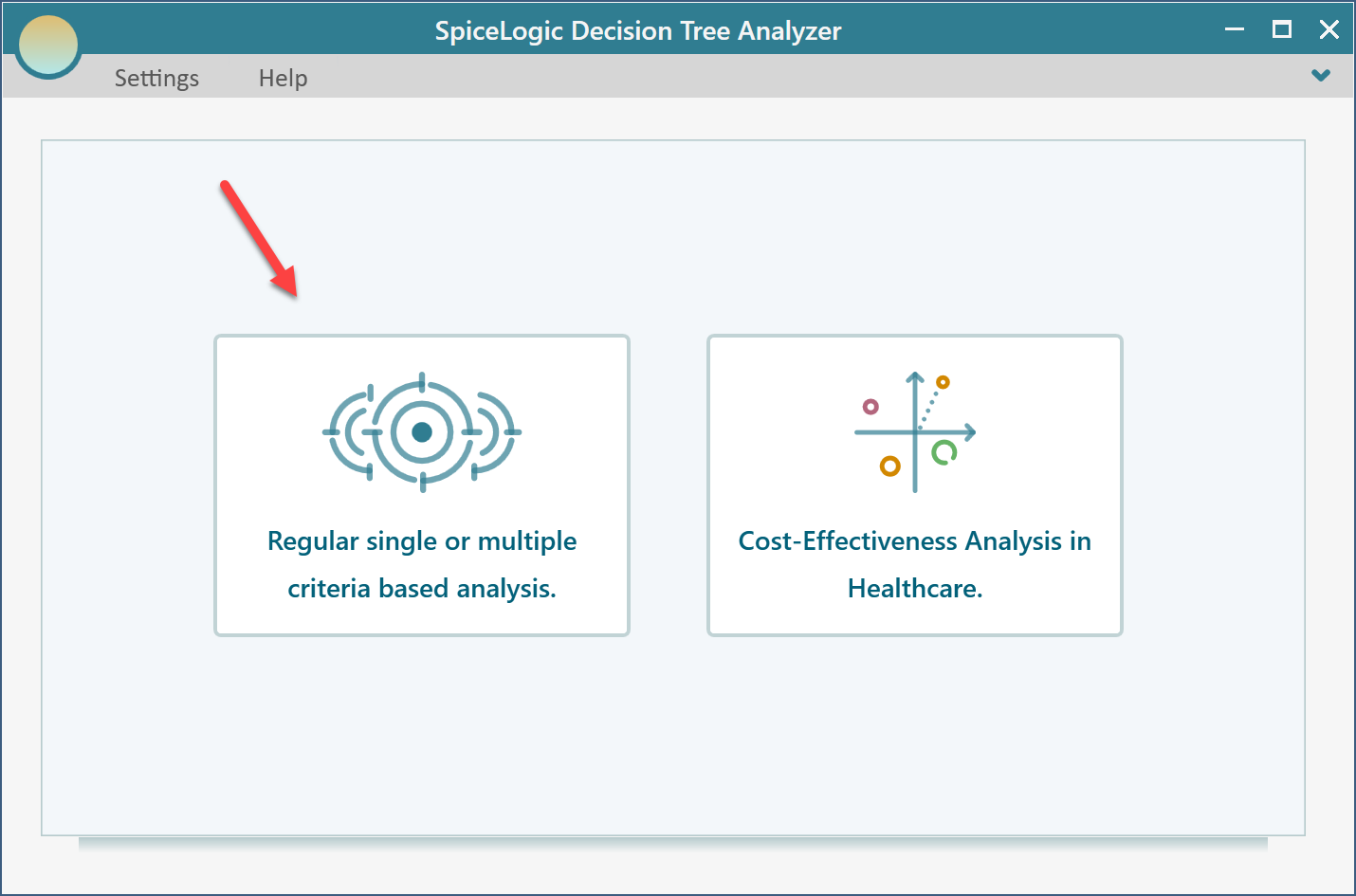
Then, you will get the following screen.
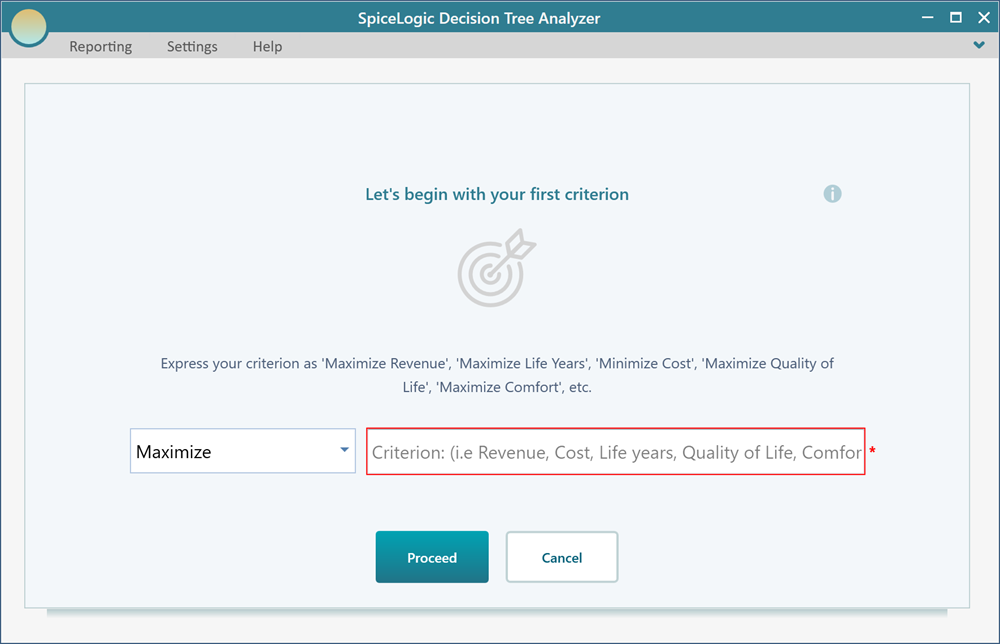
If you chose to create the decision tree first, then for the first time when you click the Payoff button from the decision tree node, you will be taken to the objective start screen, as shown above. So, you have the freedom to start with your objectives initially before making the decision tree or you can make the decision tree and then identify your objective later.
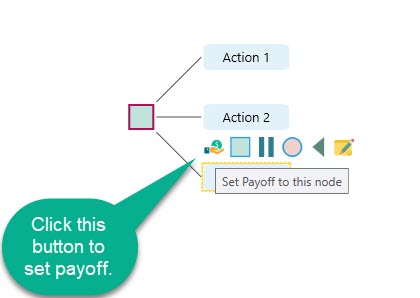
Criteria are needed to be set up only to set payoff. Therefore, until you are ready to set payoff to a node, you can easily continue with making a decision tree without identifying your objectives.
You need to structure your objectives in such a way so that your criterion can be easily identified. In a word, you need to model your objectives like this:
- Maximize Sale
- Minimize Cost
- Minimize Time
etc.
Once you model your objective like that, your criteria can be extracted easily as "Sale", "Cost", "Time", "Distance", "Neighborhood is good" etc.
In the Objective startup screen, select the appropriate objective term from the drop-down box, and enter the criterion in the textbox, as shown below.
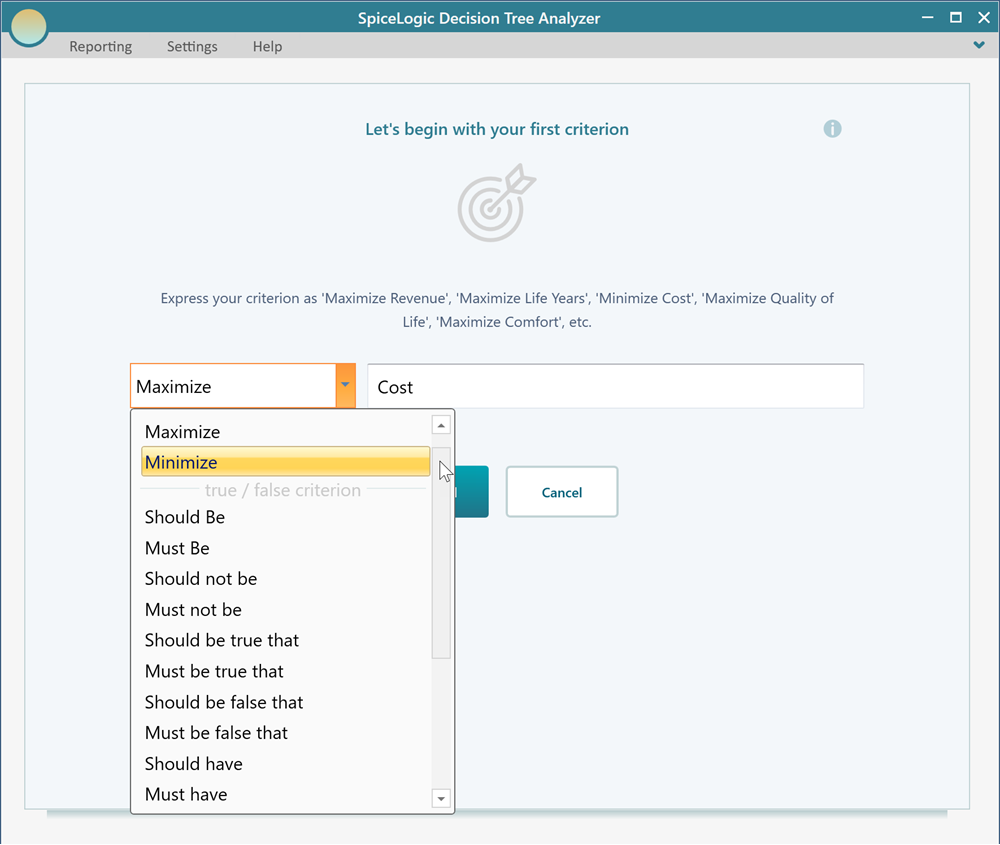
Once you enter the criterion, click the button "Proceed". Then you may be asked, what is the type of objective? It basically asks if the objective is a Number type or Subjective type.
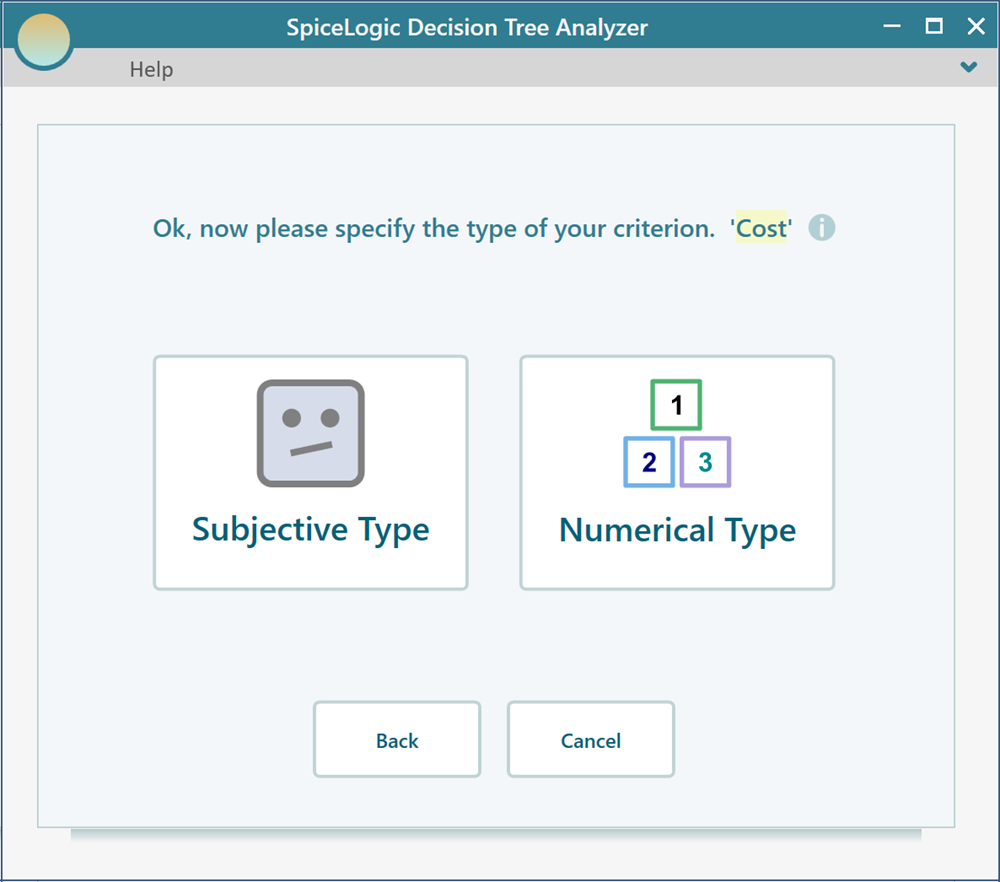
There is a reason for this question. If you want to express your payoff for something which is a subjective type (like beauty, comfort, satisfaction, etc), or if you simply want to express the payoff directly in terms of utility value (even for money) then you can choose the Subjective type. If you choose the Subjective type, then no more questions will be asked. But if you choose the Number or Monetary type, then you may be asked the Minimum possible value, Maximum possible value, unit, etc. We have explained the criterion data types and usages in detail on separate pages.
How the Multi-Criteria Payoff calculated
When you have a single objective, you will have a single criterion for a payoff. For example, Say, your objective is to Maximize Sales. Then when you set the payoff to a node, you will simply enter the Sale amount (perhaps in dollar or other currency). But when you have more than one objective, we need a way, to sum up, the criterion payoff into a single number. But, you can not add an Apple to an Orange. Similarly, different objectives' payoffs cannot be combined/summed up.
For example, say you are choosing a house to buy and you have 2 objectives.
- Minimize Distance from Work
- Maximize Area (in square feet)
Say, for a house named "house A", you have collected the distance from work as 10km. You have also measured the area as 1500 square feet. Of course, you cannot add up to 10km with 1500 square feet like 10 + 1500, right? So, you need to convert them into a common utility scale. Say, 10km can be mapped to a utility value of 0.7. And say, 1500 square feet can be mapped to a utility value of 0.4. Then say, you care about the Area 3 times more than the distance from work. Therefore, we can say, on a relative scale of 0 to 1, you have the weight for Area = 0.75 and you have the weight for Distance is 0.25. Because, 3 : 1 means, 75% : 25%.
Now, you can sum up the value for House A according to the following formula:
Value of an Action = Sum of (Objective Weight * Utility value for that objective)
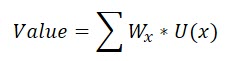
According to that formula, the overall utility value for "house A" will be
= weight of area * utility value of the area + weight of distance * utility value of distance.
= 0.75 * 0.4 + 0.25 * 0.7 = 0.475
Same way, we can compute the overall Utility value of other house options and select the one that has the highest overall utility value.
So, we need to convert all payoff to a utility function (either you define a utility function, or behind the scene, the software will create a risk-neutral utility function for you). Once the utility functions are defined, we need a way to sum the utility functions based on some weights for the objectives. The weights are evaluated based on the priority you define. Weight is a fraction number between 0 to 1 such that the sum of all weights is equal to 1.
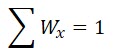
In order to calculate the overall utility value for a node, you need a way to evaluate the weights for objectives.
One way of evaluating priorities is to let the user do a pairwise comparison among various objectives and solve a matrix for Eigenvector using the algorithms used in the Analytic Hierarchy Process. Another way is to define the weights directly.
Evaluating weights by pairwise comparison
Ok, so once you chose the type of objective, you will be asked if you have another objective.
If you answer "No", then things are straightforward and simple. In a decision tree, you will be able to enter the payoff based on that single criterion. But say, you have more than one objective, then answer "Yes". Then you will be able to enter another objective the same as you did for the first one. Once you are done with all objectives, then you will answer "No" to the screen as shown above. Then, you will be taken to a pair comparison window as shown below.
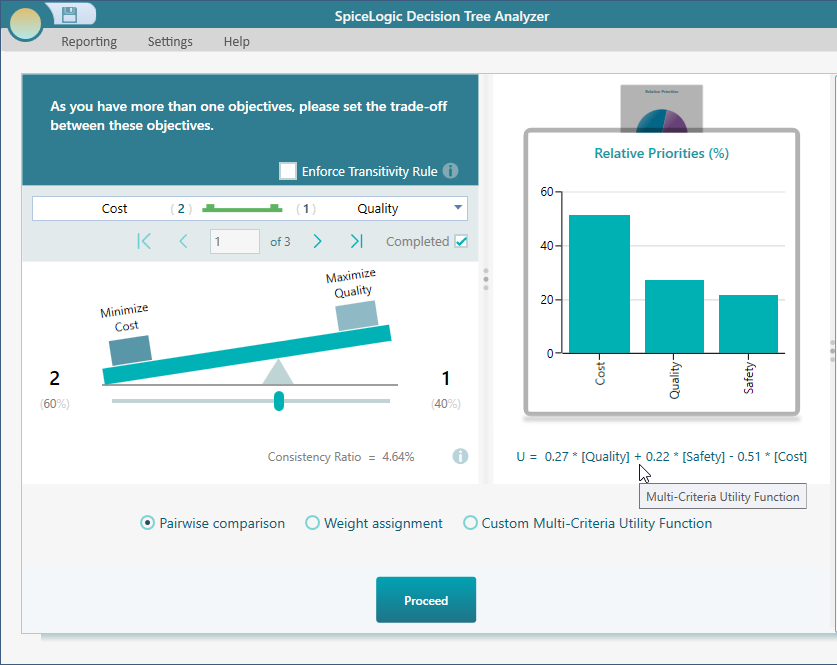
Pairwise Comparison Explained
As you can see, it is a very intuitive user interface where you can express your priority one over another using the weight scale. For example, if you prefer to minimize cost 2 times as much as you prefer to maximize quality, then you can set the slider as shown below.
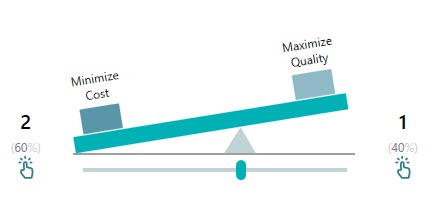
In that way, you can set up all the tradeoffs one by one. Once a comparison is completed (as soon as you move the slider) you will see the following checkbox gets checked, which indicates that this comparison is completed.
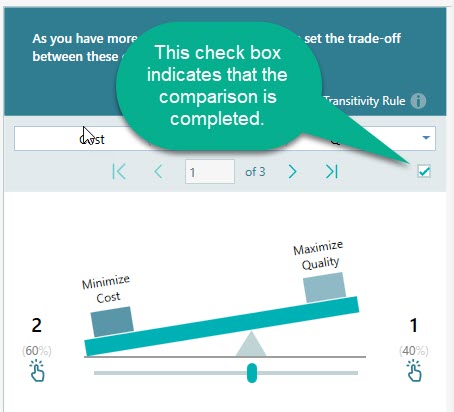
That status is set based on your slider movement. But if you really want to set the priorities equal (1:1) then you can manually check that checkbox to mark it as completed. You can navigate to the next pair comparison by clicking the navigation buttons on the toolbar.
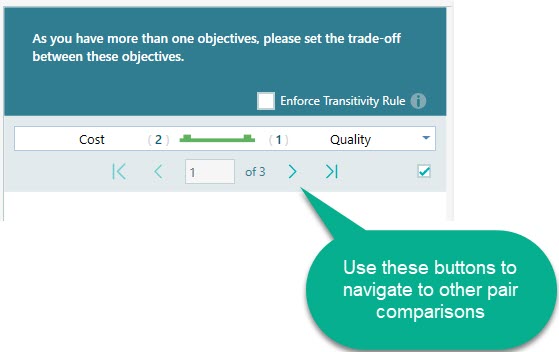
You can expand the drop-down to jump to a pair directly.

Weight for an objective will be calculated using the same Eigen Value algorithm that is used for the Analytic Hierarchy Process. The relative weight will be reflected in the chart which is displayed in the same panel as shown below.
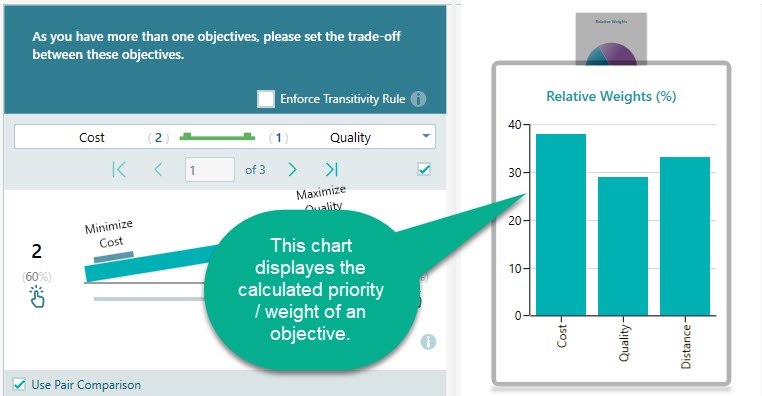
You will also find a Pie chart in the same carousel as shown below.

Consistency Ratio Metric
The consistency-Ratio metric basically tells you how much you violate the transitivity rule. Let me explain. Suppose you like an apple twice as much as an orange and an orange 3 times as much as a banana. If your preference between an 'apple' and a 'banana' does not reflect that proportion, then you are said to be inconsistent in your preferences. Consistency ratio measures such inconsistency. The higher this number, the more inconsistent you are. When you are 100% consistent in your preferences, the deviation will be 0.
Notice the number shown at the bottom of the comparison weight slider.
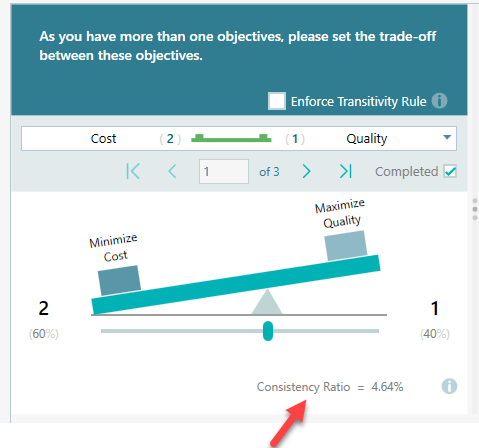
According to Thomas L. Saaty, the consistency ratio should be less or equal to 10%. So, if you notice your consistency ratio is over 10%, it is necessary to revise your judgments. In such a case, the software will indicate that using a Red bold color, as you can see on this screen.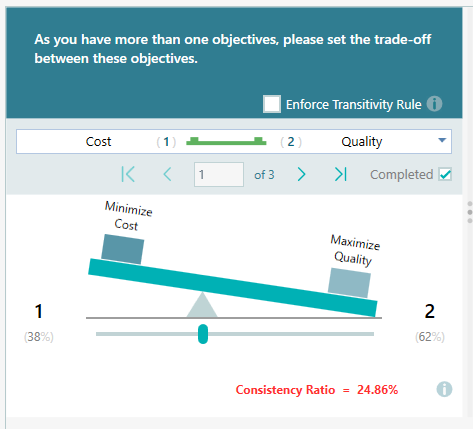
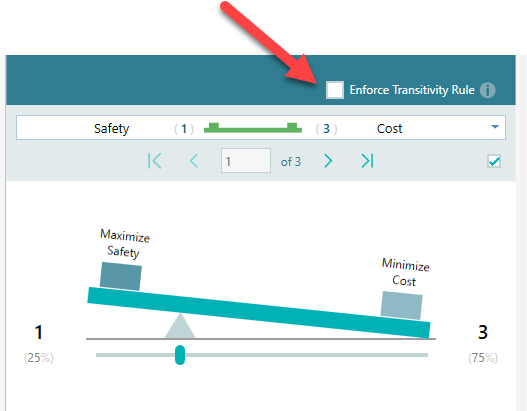
Enforce Consistency (Transitivity Rule)
It is possible using our software that you can enforce consistency in all pair comparisons. That means, instead of asking you to compare apple-orange, apple-banana, and orange-banana, the software will ask you just 2 comparisons to perform. Apple-orange and apple-banana. Then it will infer the comparison of orange-banana. In that way, you can reduce the number of comparisons from ½ * n * (n -1) to just (n -1). Think about it. It can be a huge time-saver for you as the number of comparisons gets reduced dramatically. You can enforce the Transitivity rule by checking this checkbox. As soon as you do so, you will see the number of pair comparisons has been reduced significantly.
Setting Objective weights directly
At times, you may want to expedite your decision-making process by bypassing the pairwise comparison and setting the priority weights directly for your objectives. You can do that by selecting the weight assignment option as shown below.
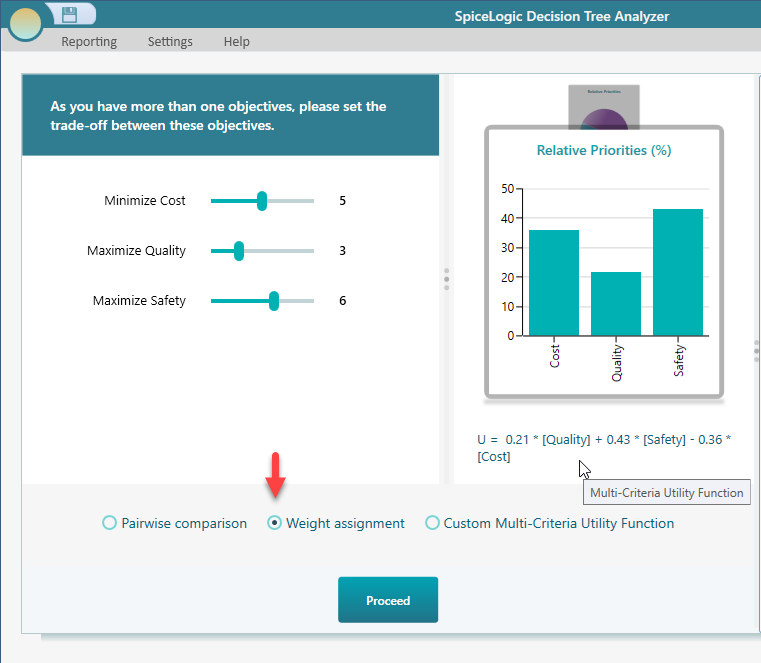
Once you do that, you will see a panel with the list of Objectives along with a slider so that you can express your priority for that objective. The slider will let you express the priority between 1 to 9. Then, it will calculate a relative proportion fraction such that,
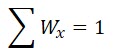
For example, the above 3 objective weights will be calculated as
The weight of "cost" = 5 / (5 + 3 + 6) = 0.36
Weight of "quality" = 3 / (5 + 3 + 6) = 0.21
Using Custom Expression for Multi-Criteria Utility Function
You may like to use a custom expression for your multi-criteria utility function, like
= 2 * [Quality] - 3 * [Cost] + 7 * [Safety]
or a sophisticated function like
= sqrt( [cost] ) + e^( [safety] / log10( [quality] ) )
Yes, you can do that. Simply check the box labeled "Custom Multi-Criteria Utility Function", as shown below.
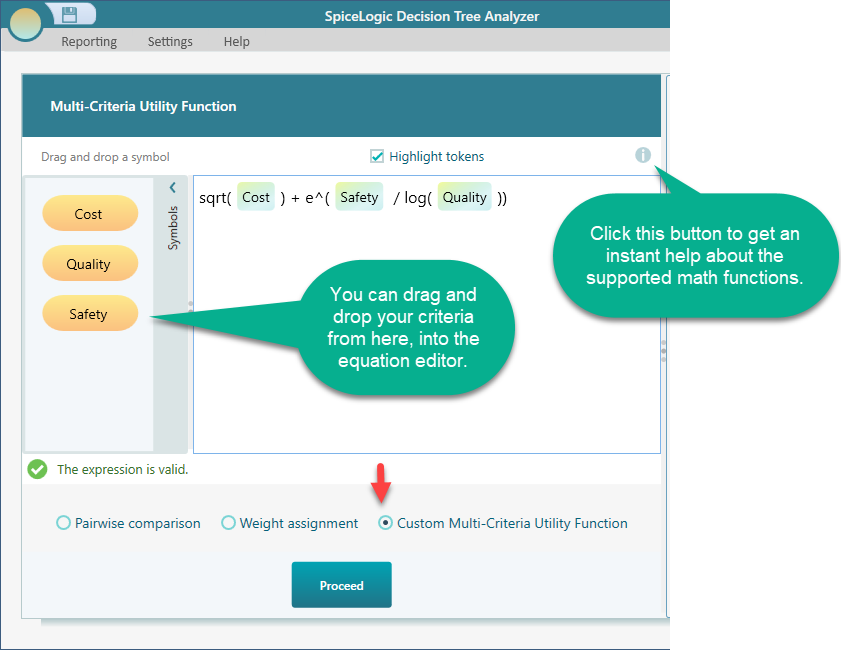
Please note that, if you want to model a utility function for individual criteria, you can do that here too. But, it is not recommended to do that here. Rather, you can create a rich utility function for individual criteria from the objective editor, as explained on the Utility Function page.
This equation editor is a rich editor and it should be good enough to create any mathematical expression you may need to create as a Utility function.
As shown in the above screenshot, there is a help button that will help you to get a quick idea about what math functions are supported. Here is the screenshot of the popup that is displayed when the help button is clicked.

Managing Criteria
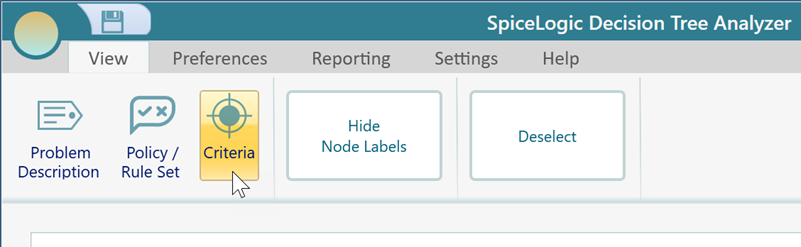
Once you have created a list of Criteria, you can navigate to the Criteria page anytime from the Decision Tree window. Look into the Ribbon's View tab and you will find a button "Objectives". Click that button to navigate to the objectives page.
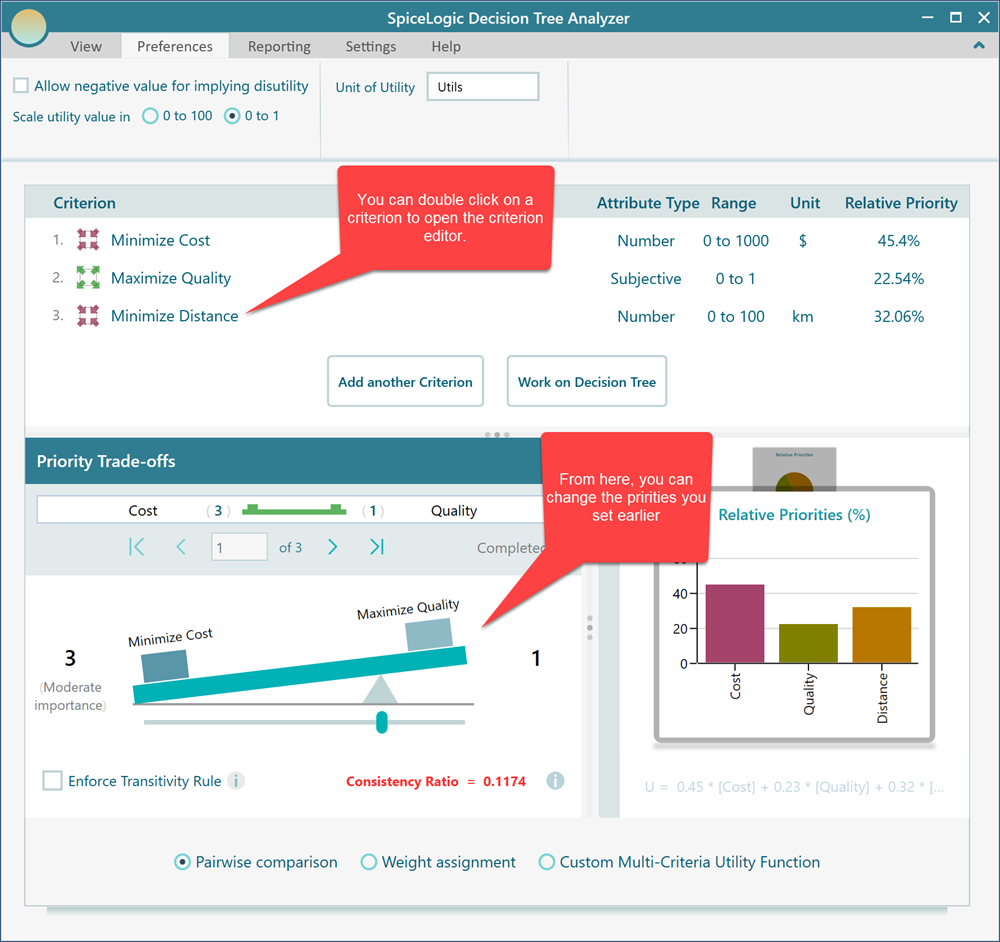
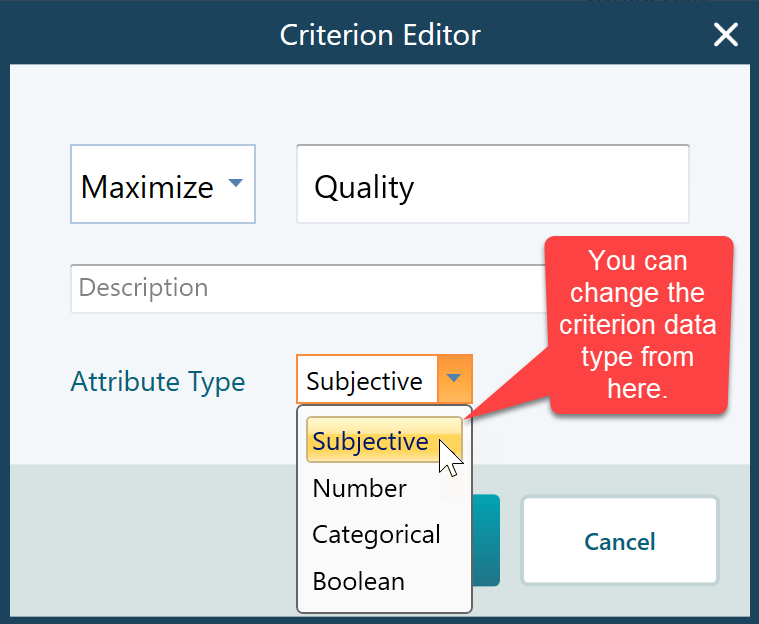
On the criteria page, you will see the list of criteria. You can double-click on any criterion to open the criterion editor. Based on the data type of the criterion, a dedicated criterion editor will show up.
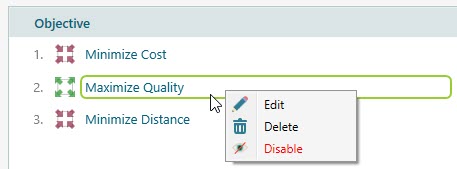
You can also right-click on a criterion item to see its context menu, and from that context menu, you will find the Edit and Delete option.
Not only from the criteria manager, but you can also open a criterion editor directly from the Decision Tree Payoff popup. In the payoff popup, you will see the list of criterion values as shown below.
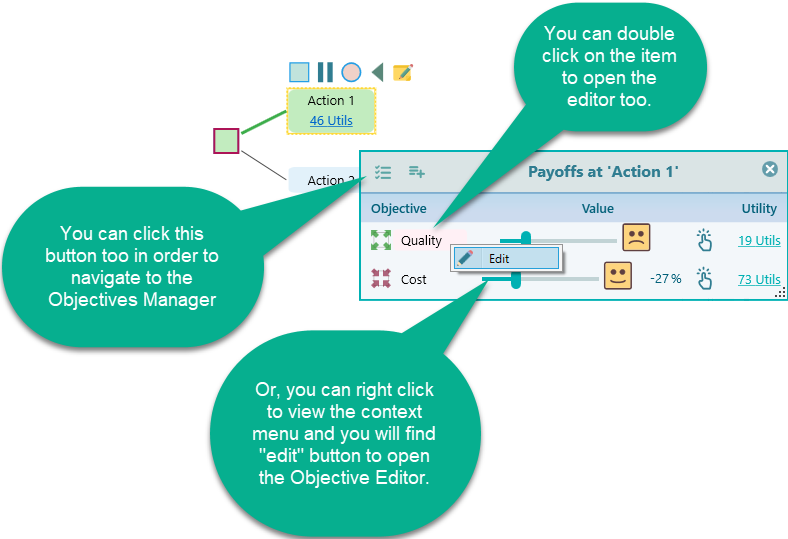
Criterion Editor
As mentioned, depending on the Objective data type, you will see different Criterion editors when you double-click to edit the objective. This is a screenshot of the Criterion Editor for the Subjective type.
Disable a criterion
You see that you can disable a criterion as well from the context menu.

If you disable a criterion, the criterion will not take part in the calculation. It is very useful in a way that, say you want to check what if you sacrifice a criterion, and how the final decision is altered. Later, you can enable the criterion. If you delete a criterion, then you cannot get that back. So, disabling is a very useful feature for what-if analysis.
