Example: Gambler's ruin
It is the famous Gambler's ruin example. In this example, we will present a gambler. A reluctant gambler is dragged to a casino by his friends. He takes only 50$ to gamble with. Since he does not know much about gambling, he decides to play roulette. At each spin, he places 25$ on red. If red occurs, he wins 25$. If black comes up, he loses his 25$. Therefore, the odds of winning are 50%. He will quit playing when he either has 0 money left or is up to 25$ (75$ total). Let's model this process as a Markov Chain and examine its long-run behavior.
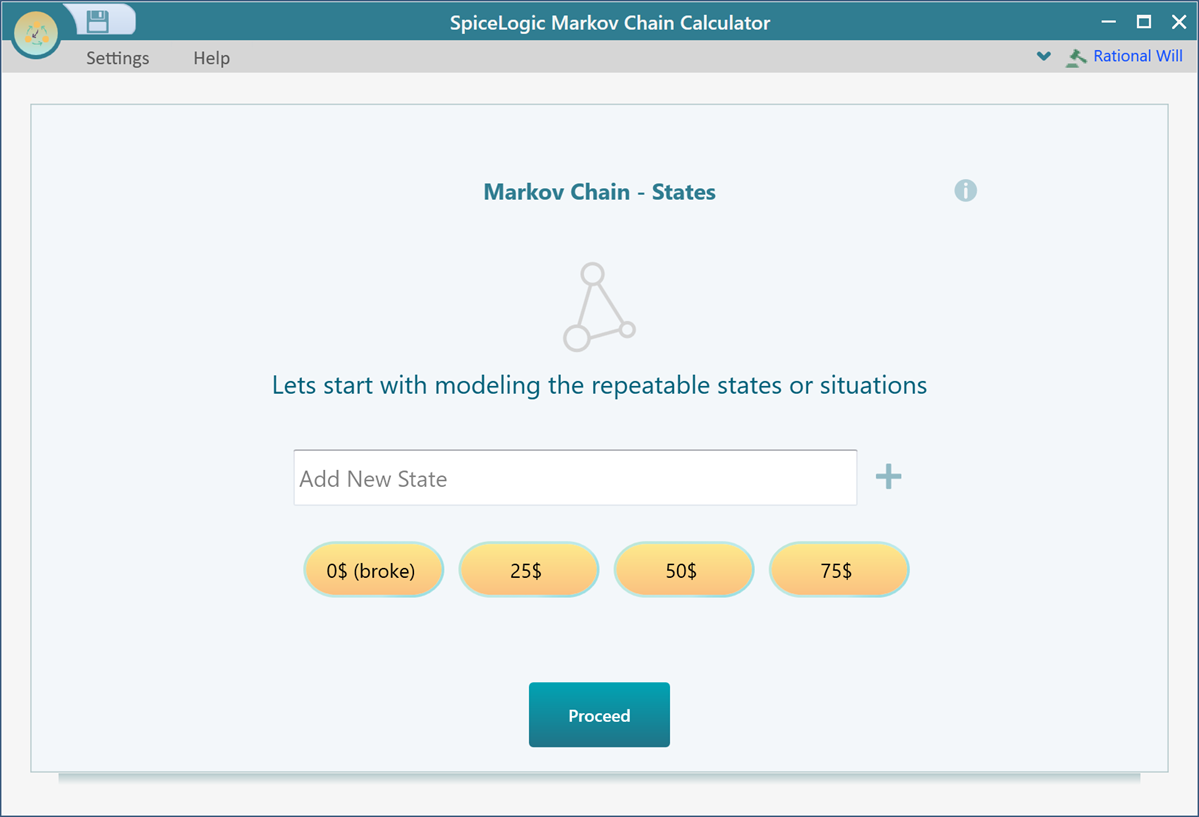
Start the SpiceLogic Markov Chain Calculator and enter four states as shown below.
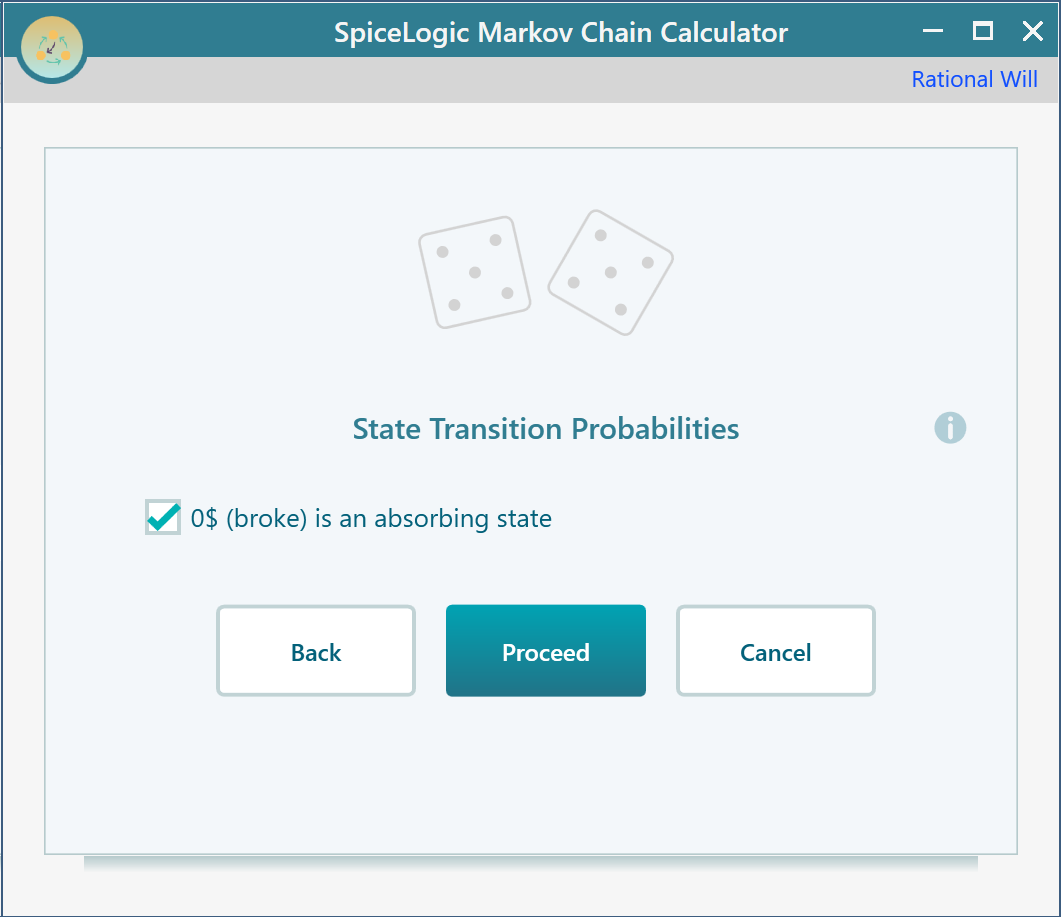
Once you click Proceed, you will be asked to set the probability for state 0$ (broke). As 0$ (broke) is an absorbing state (as you cannot move to another state after you are broke), set this state as an absorbing state.
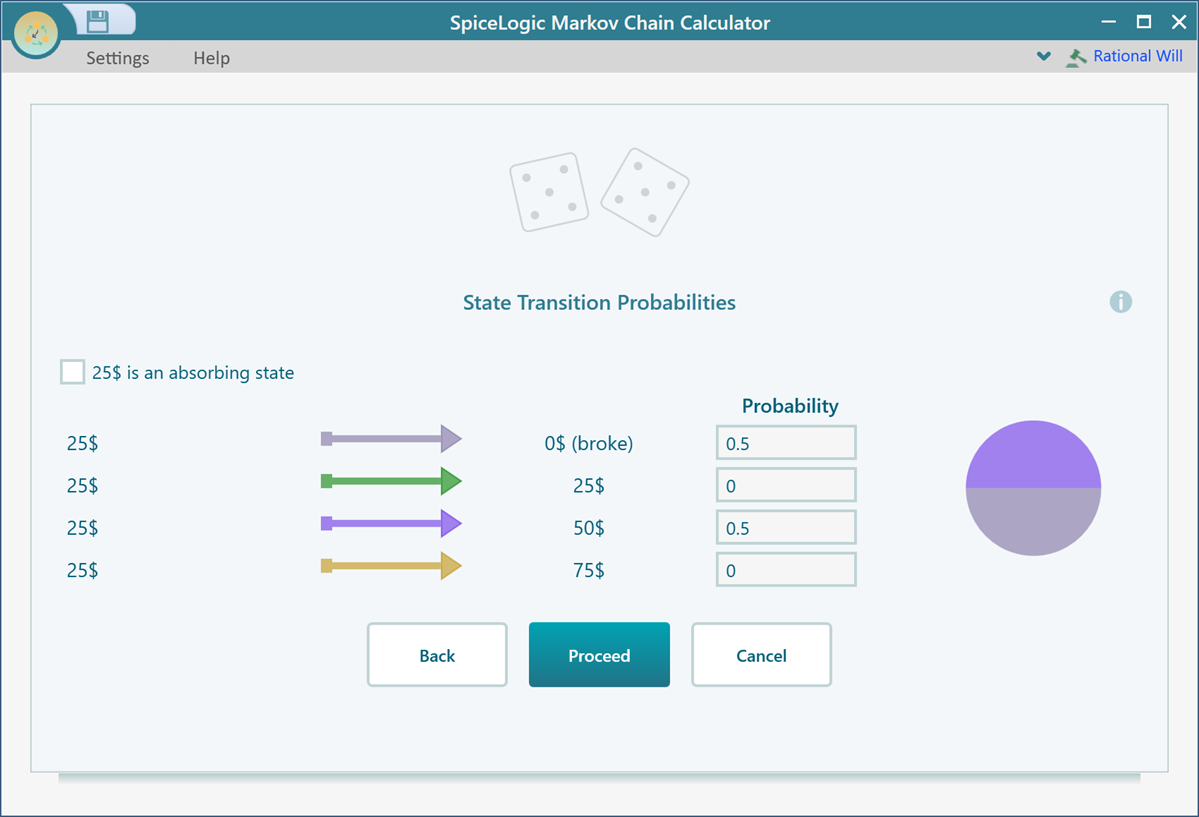
Then click Proceed and set the transition probability of 25$ state as shown below.
Then click Proceed and set transition probabilities for the state 50$ as shown below.
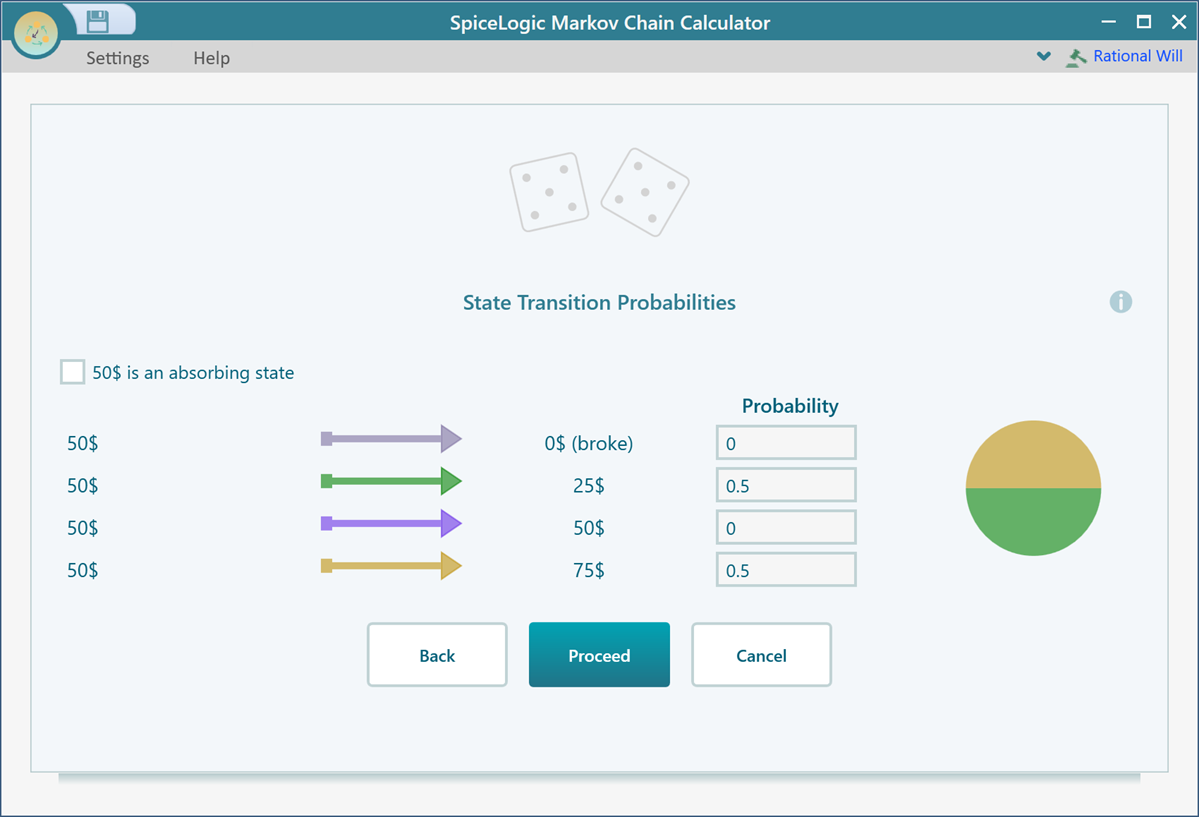
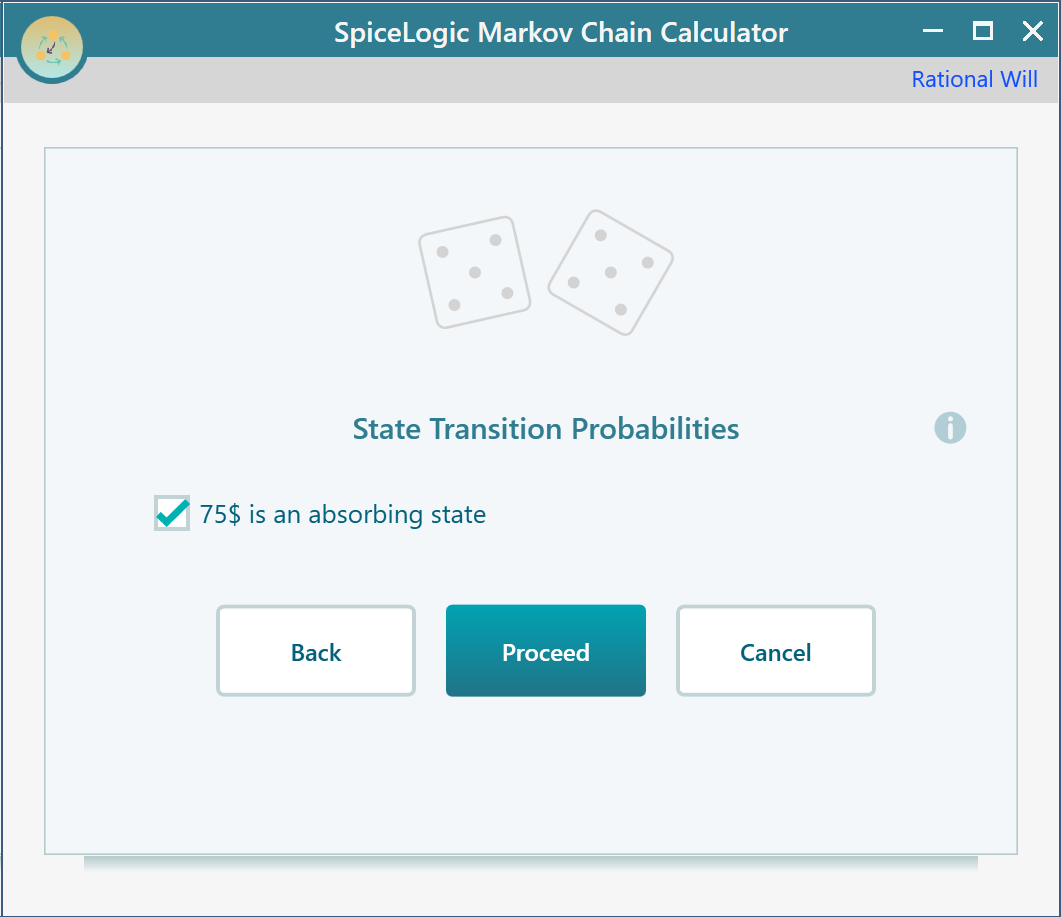
Finally set 75$ state as the absorbing state. Because, once the gambler reaches 75$, he quits the game.
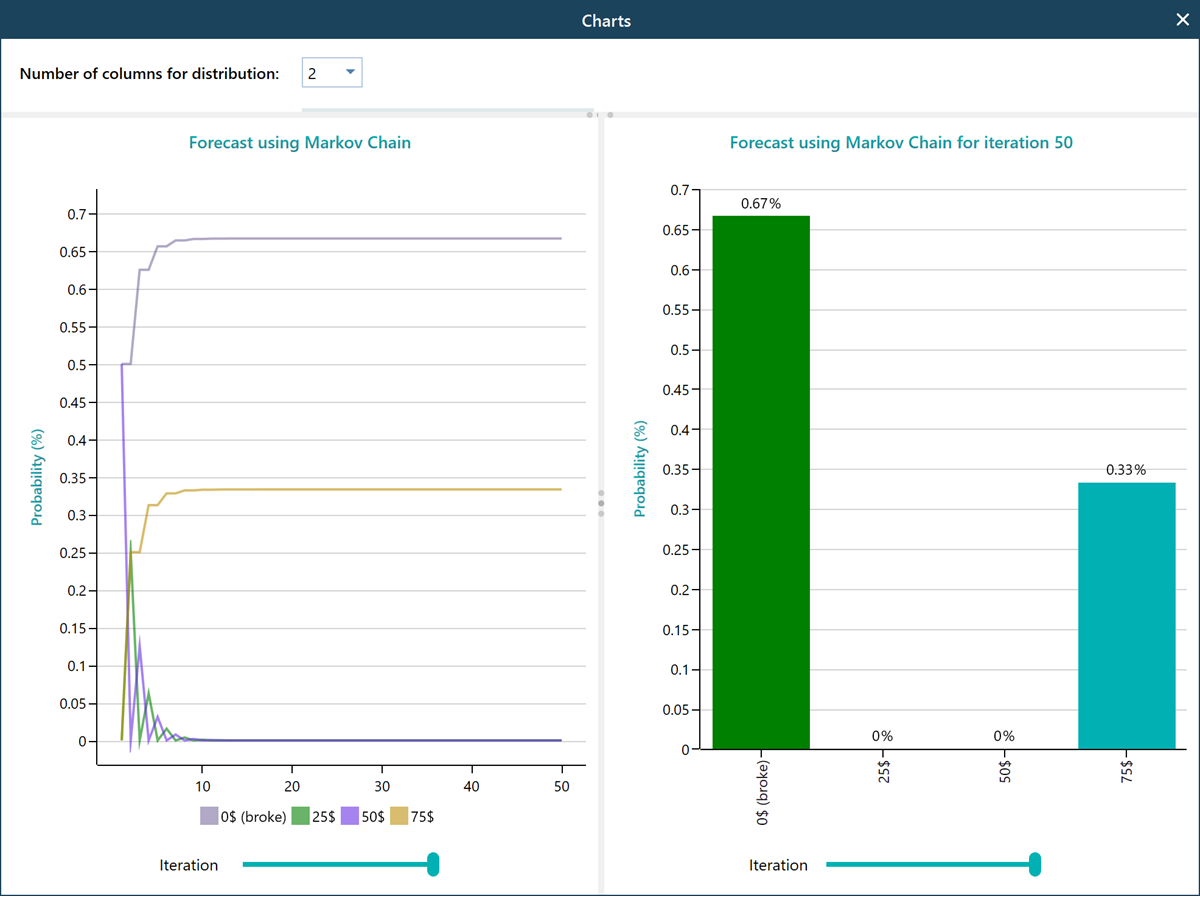
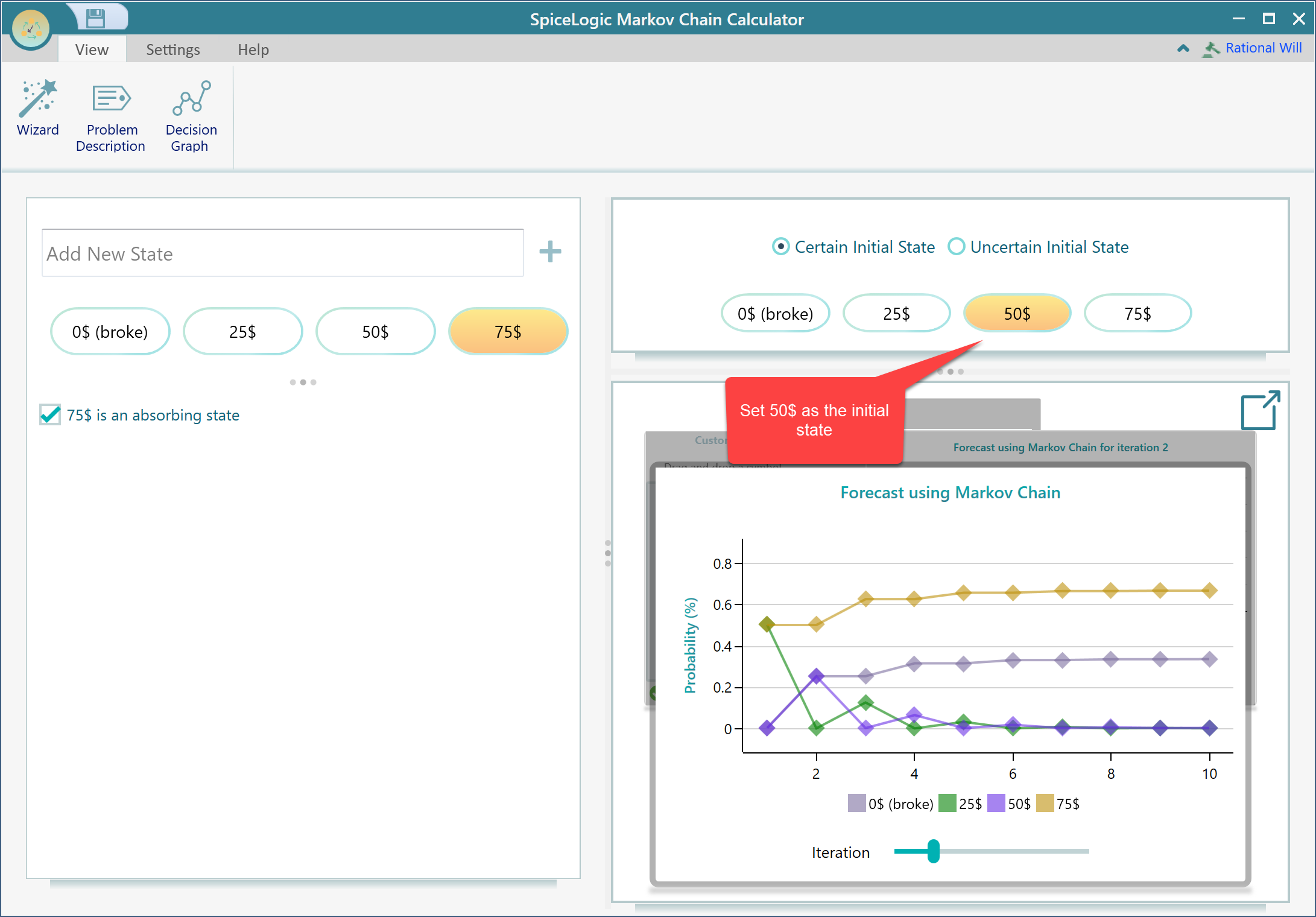
Then click Proceed and then click the Finish button in the final wizard screen. Then you will get the following result view. You need to set a certain initial state to perform the analysis. Let's assume that the gambler starts with 50$. So, select 50$ from here.
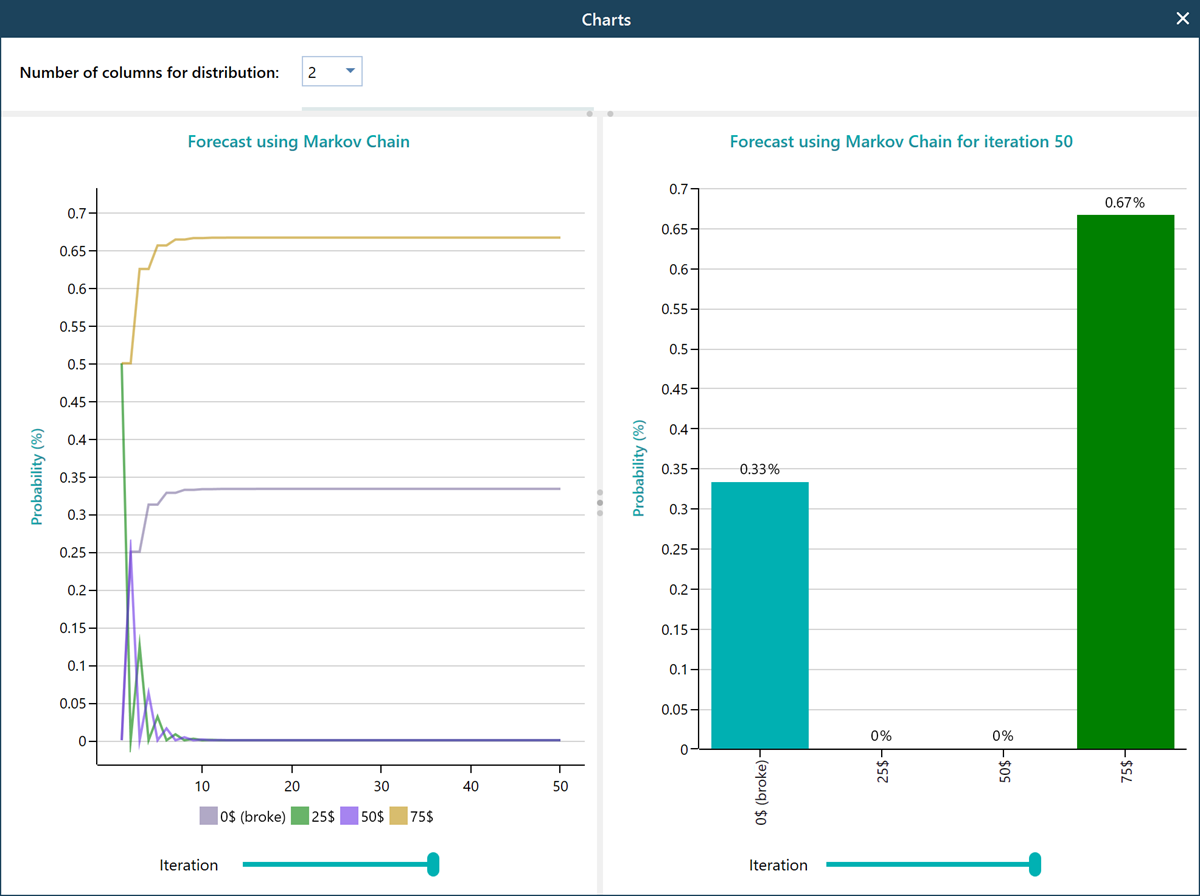
Pop out the charts from the carousel Change the slider to 50 iterations and observe that, after 50 turns, the probability of getting broke is 33%, and getting 75$ and quit is 67%.
Now, what if the gambler starts with 25$. We can find out the forecast by selecting the initial state as 25$.
Once you change the initial state, notice that the probability of getting broke increases to 67%, and the probability of having 75$ decreases tp 33%