Getting Started with Bayesian Inference
Bayesian inference is a method of probabilistic inference in which Bayes' theorem is used to update the probability of a hypothesis. When more evidence or information becomes available, using Baye's theorem, the degree of belief in the hypotheses is updated.
Bayesian Doctor comes with a strong GUI tool for Bayesian Inference. You can systematically organize the hypothesis, experiments, and observations and finally, you can update the belief based on pieces of evidence.
In this document, we will demonstrate how we can update a belief of some hypotheses based on symptoms.
Warning: This example is not to be taken as a real clinical example. Rather, it is just an example for the purpose of easy understanding of the tool. Please consult your doctor for any real clinical reasons.
Say, you have nausea and vomiting. You are suspecting that it could be either a Peptic Ulcer or Viral Gastroenteritis.
Now, let's start with the "Bayesian Doctor" or "Rational Will" software.
Select Bayesian Inference and add your two hypotheses as shown below.
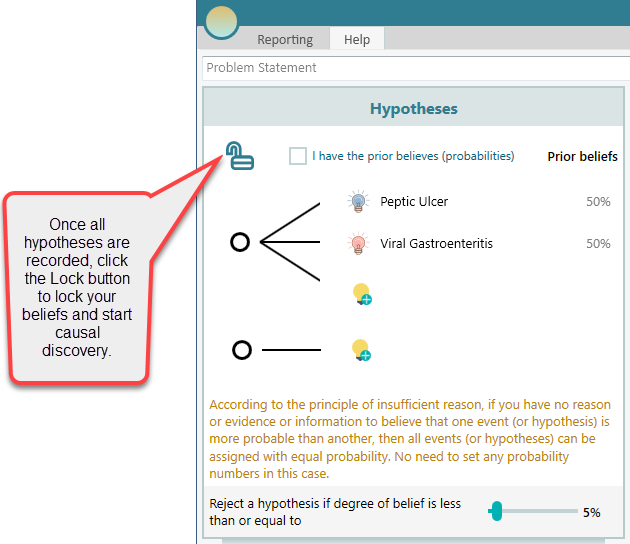
You can have your initial belief about the causes. For example, you may believe that you must have a Peptic Ulcer (maybe because a member in your family also got a peptic ulcer). Therefore, you can specify your belief on Peptic Ulcer as 70% and Viral Gastroenteritis as 30%.

But, say, you have no reason to believe one cause is more probable than the other cause, then simply uncheck that checkbox "I have the prior beliefs...". In that case, the Principle of Indifference will be applied.
Now, Click the Lock button to lock your beliefs. This lock button locks the prior beliefs and lets you update the beliefs based on experiments and observation so that you do not change the beliefs accidentally by changing the sliders in the hypotheses panel.
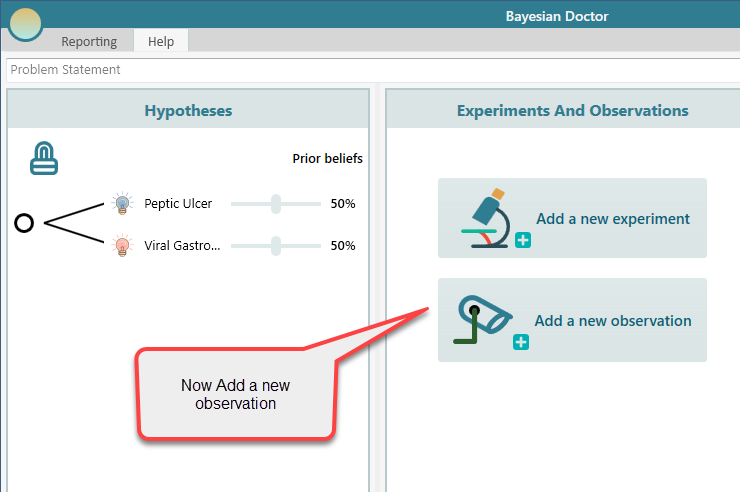
Say, you observed that you felt Nausea and Vomiting. After listing the observations, it will look like this.

Now, let's start the causal discovery.
You will see the causal discovery section below:
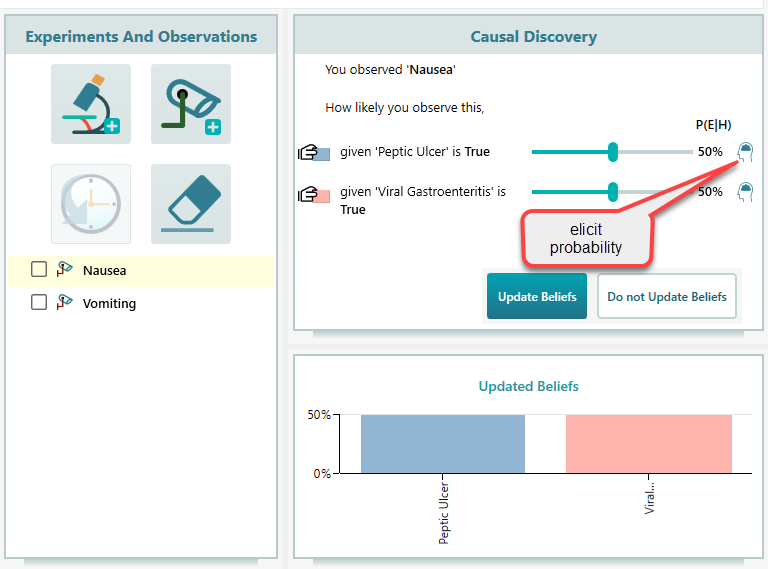
If you already know the probability of observing Nausea, when someone really has a Peptic Ulcer, then using the slider you can set that probability accordingly.
But if you do not know, you can click the elicit probability button to elicit that probability.
Once you open the Elicit window, list the symptoms of the hypothesis "Peptic Ulcer" as shown below. You should set the probability of symptoms for the given cause (diseases). Here is a random setup. (Warning: again, this is a random setup. That means, this probability is not shown based on medical information, rather it is based on personal belief. Consult medical information to find the correct probabilities for various symptoms)
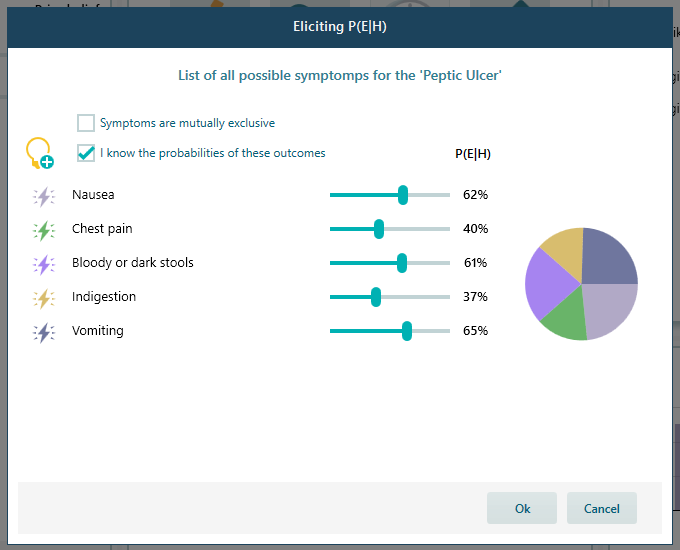
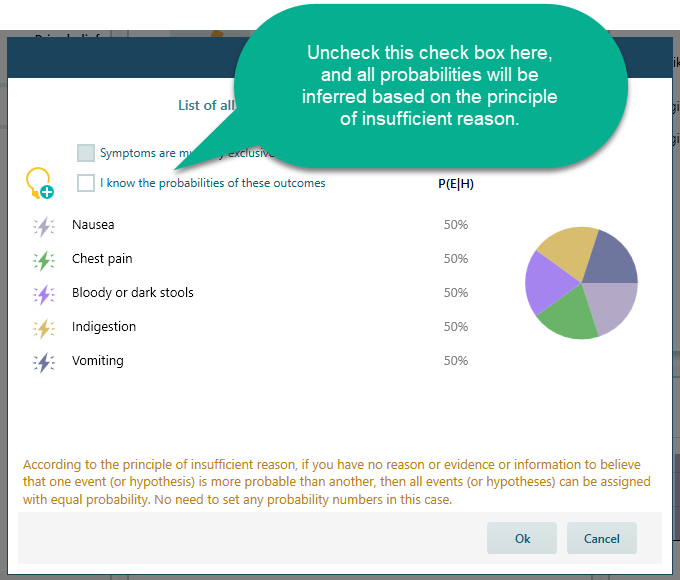
If you do not know the probability of any symptoms at all, you can let this program infer the probabilities based on the Principle of Indifference. According to the principle of indifference, if you have no reason or evidence or information to believe that one event (or hypothesis) is more probable than another, then all events (or hypotheses) can be assigned with equal probability. No need to set any probability numbers in this case.
Therefore, if you do not know the probability of any symptoms at all, uncheck the checkbox here and all probabilities of the symptoms will be assigned equally.
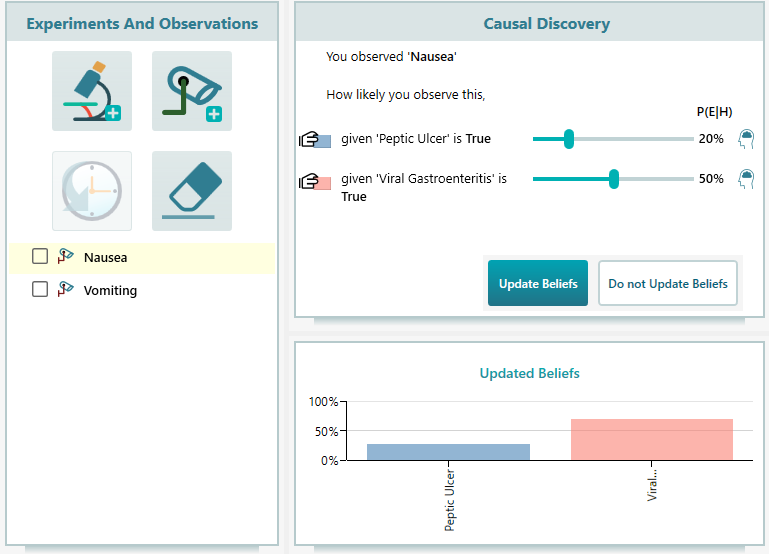
Click OK and you will see the likelihood probability is updated for nausea.
Now, do the same for Viral Gastroenteritis. Again, the probability of symptoms shown here is not based on medical information. Rather it is an example showing, how to brainstorm and update your beliefs. So, if you have some initial beliefs about some symptoms, how you can derive the probability of the root hypothesis? That's all about it. If you are a doctor and you know the probabilities of symptoms, enter the probabilities and you will get better results.
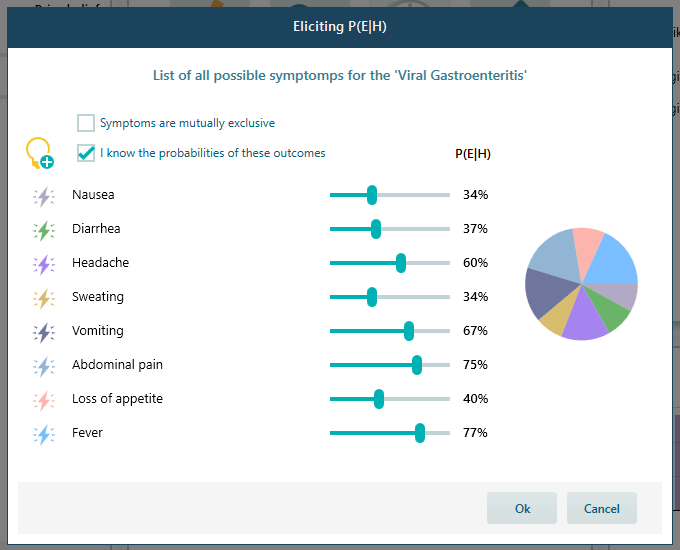
Once you click OK, the likelihood of Viral Gastroenteritis will be updated as shown below. Please note that most of the time, you may not need to open that Elicit window, rather, you can directly realize the likelihood of observation when a given Hypothesis is True.
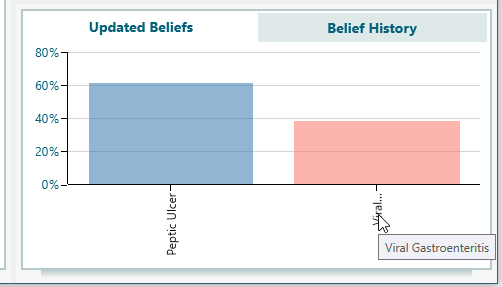
Once you click the Update Beliefs button, your hypotheses will be updated according to Baye's theorem as shown below.
Same as Nausea, do the Causal Discovery for Vomiting and update the beliefs.
Once you update the beliefs, the final result of Bayesian Inference will be shown up like this:
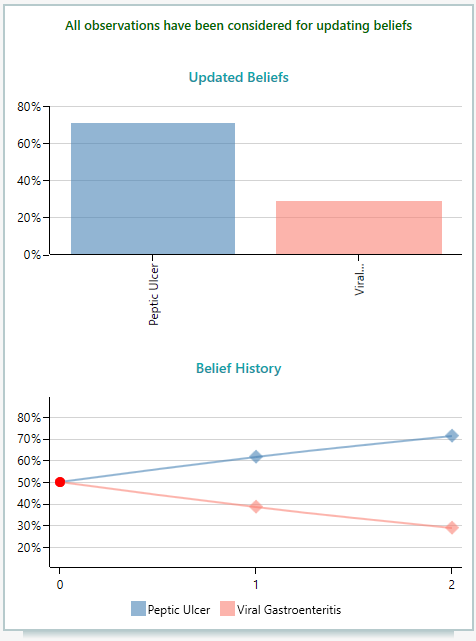
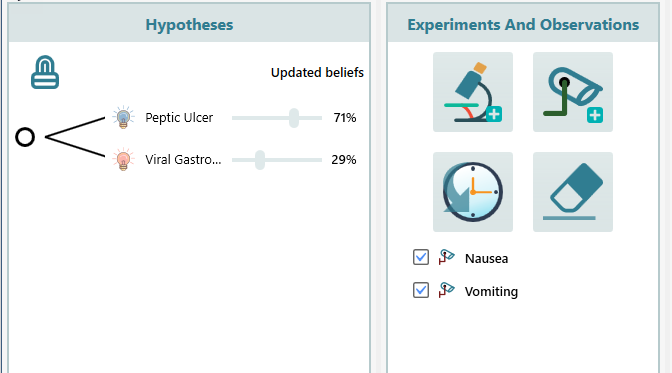
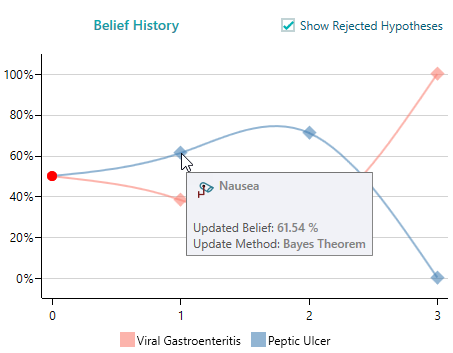
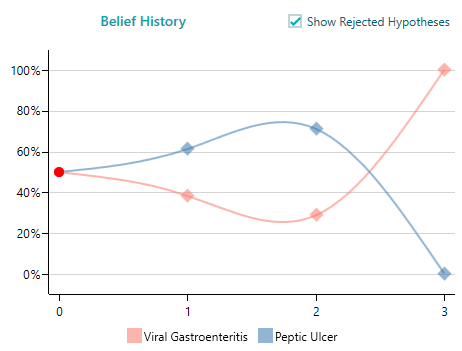
So, you can see that your belief in Peptic Ulcer is updated as 71% and the belief in Viral Gastroenteritis is updated as 29%. So, until now, you can think that there is a high chance that Peptic Ulcer is the cause. Also, notice the Belief history, which shows how your beliefs were updated over time.
Then, the next day, you started to experience a fever. So you include that observation and perform the causal discovery session again. Notice that, fever is not on the list of possible symptoms for Peptic Ulcer, so we set the likelihood of fever given Peptic Ulcer is 0%. But, as fever is one of the symptoms of Viral Gastroenteritis, we can set the likelihood of fever given Viral Gastroenteritis is true, as 13%.
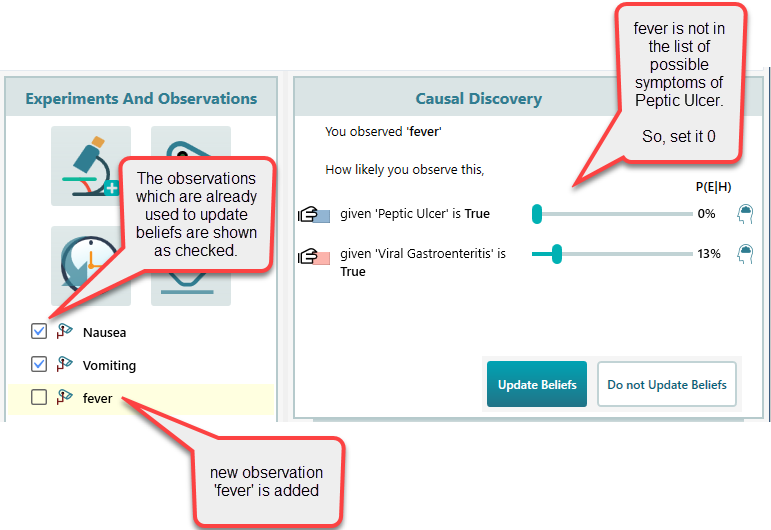
Now, click the Update Beliefs button. You will see the following updated beliefs.
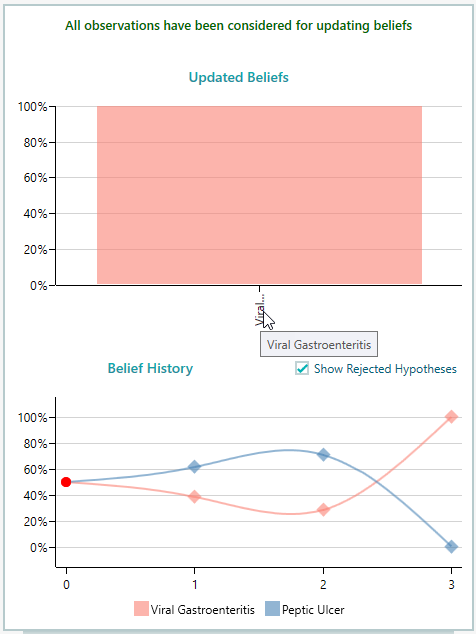
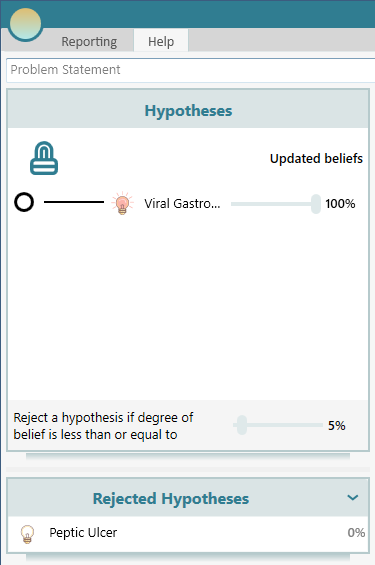
This time, the hypothesis of 'Peptic Ulcer' is rejected.
Notice the Belief history chart. The belief of Peptic Ulcer went higher by 2 observations and then went down all the way 0 after the 3rd observation. That is a true example of Diachronic Interpretation. Updating beliefs over time, upon evidence.
The tooltip on the data point in the Belief History also shows the observations that caused the belief change.